CF2122F Colorful Polygon

给定一个数组 $a_1, a_2, \ldots, a_n$，其中 $n \leq 8$，并且 $a_1 + a_2 + \cdots + a_n \leq 100$。 请你构造一个**简单多边形** $^{\text{∗}}$，顶点数不超过 $333$，使得它恰好有 $$ \frac{(a_1 + a_2 + \cdots + a_n)!}{a_1! a_2! \cdots a_n!} $$ 种不同的**三角剖分** $^{\text{†}}$。可以证明总是存在这样的多边形。 $^{\text{∗}}$ 一个[简单多边形](https://en.wikipedia.org/wiki/Simple_polygon)是指没有自交且没有洞的多边形。换句话说，任意两条非相邻边没有公共点，相邻边恰好有一个公共点（即它们之间的顶点）。相邻边可以共线。 $^{\text{†}}$ 一个多边形的[三角剖分](https://en.wikipedia.org/wiki/Polygon_triangulation)是指选出 $m-3$ 条对角线（$m$ 为顶点数），这些对角线只在顶点处相交。对角线是指多边形内部连接两个顶点的线段，且仅与多边形的边在端点处重合。

每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 8$），表示数组的元素个数。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \leq a_i \leq 100$），表示数组元素。 保证 $a_1 + a_2 + \cdots + a_n \leq 100$。

第一行输出一个整数 $m$（$3 \leq m \leq 333$），表示多边形的顶点数。 接下来 $m$ 行，每行两个整数 $x_i, y_i$（$-10^6 \leq x_i, y_i \leq 10^6$），表示第 $i$ 个顶点的坐标。 多边形必须是简单多边形。顶点顺序可以是顺时针也可以是逆时针。

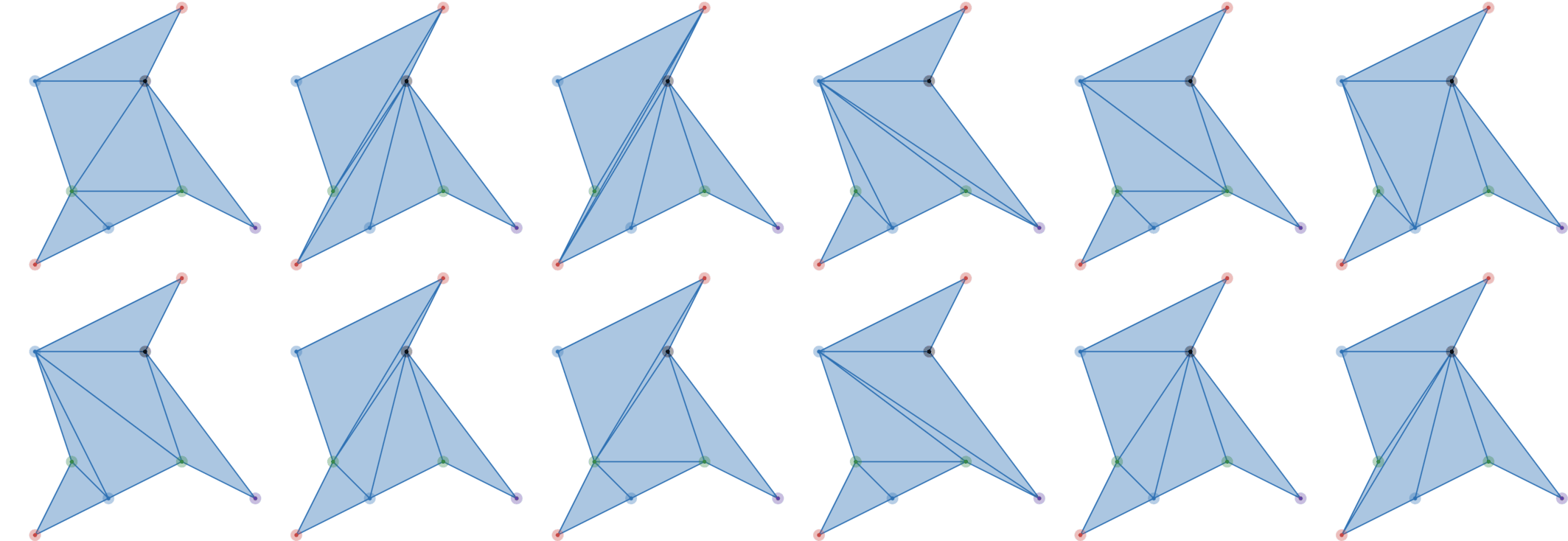
在第一个样例中，所需多边形必须有 $\tfrac{4!}{1! 1! 2!} = 12$ 种三角剖分。下图展示了该多边形的所有三角剖分：  在第二个样例中，所需多边形必须有 $\tfrac{5!}{4! 1!} = 5$ 种三角剖分。  翻译由 ChatGPT-4.1 完成。