CF2122F Colorful Polygon

You are given an array $ a_1, a_2, \ldots, a_n $ , where $ n \leq 8 $ and $ a_1 + a_2 + \cdots + a_n \leq 100 $ . Construct a simple polygon $ ^{\text{∗}} $ with at most $ 333 $ vertices that has exactly $\frac{(a_1 + a_2 + \cdots + a_n)!}{a_1! a_2! \cdots a_n!} $ different triangulations . It can be proven that such a polygon always exists. A [Simple_polygon](https://en.wikipedia.org/wiki/Simple_polygon) is a polygon that does not intersect itself and has no holes. In other words, no two non-consecutive edges can have common points, and consecutive edges must have exactly one common point — the vertex between them. Consecutive edges may be collinear. A [Polygon_triangulation](https://en.wikipedia.org/wiki/Polygon_triangulation) of a polygon with $ m $ vertices is a set of $ m-3$ diagonals that intersect only at vertices. A diagonal is a segment between two vertices which lies inside the polygon and has exactly two common points with the polygon sides — the vertices it connects.

The first line of each test contains a single integer $ n $ ( $ 2 \leq n \leq 8 $ ) — the number of elements in the array. The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \leq a_i \leq 100 $ ) — the elements of the array. It is guaranteed that $ a_1 + a_2 + \cdots + a_n $ does not exceed $ 100 $ .

In the first line, output a single integer $ m $ ( $ 3 \leq m \leq 333 $ ) — the number of vertices in the polygon. In the $ i $ -th of the following $ m $ lines, output two integers $ x_i $ , $ y_i $ ( $ -10^6 \leq x_i, y_i \leq 10^6 $ ) — the coordinates of the $ i $ -th vertex of the polygon. The polygon must be simple. The vertices may be given in either clockwise or counterclockwise order.

In the first test, the required polygon has to have $ \tfrac{4!}{1! 1! 2!} = 12 $ triangulations. The following are all the triangulations of the example polygon. 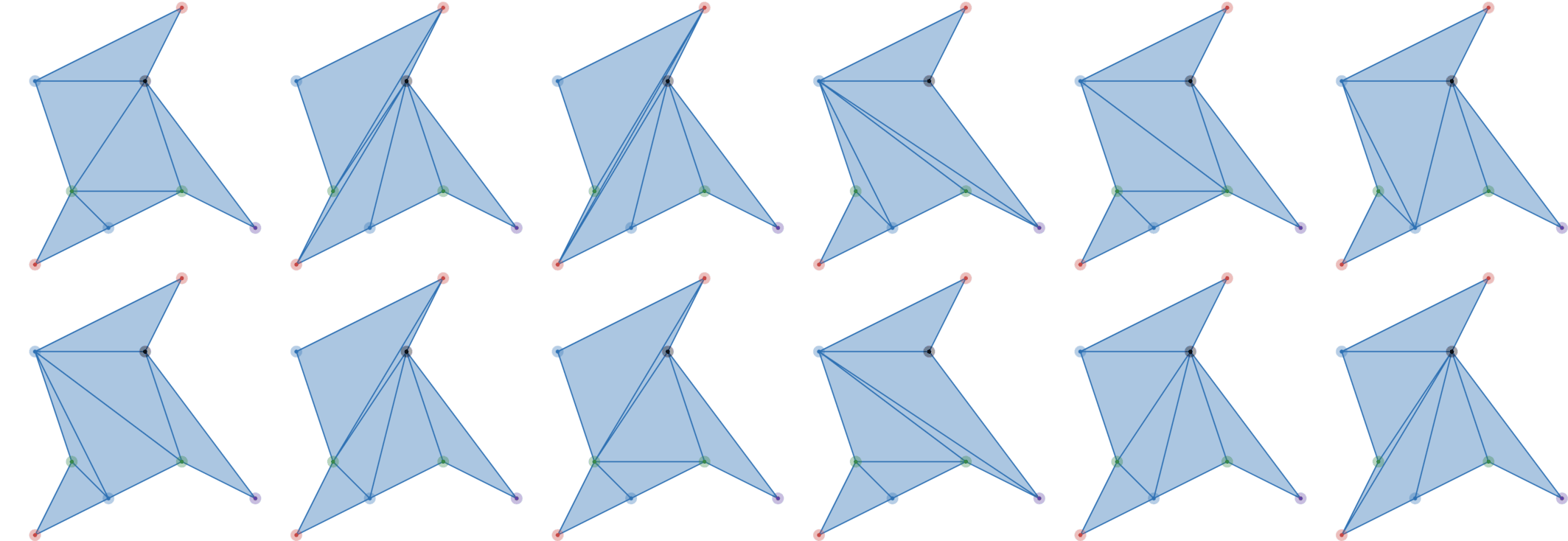 In the second test, the required polygon has to have $ \tfrac{5!}{4! 1!} = 5 $ triangulations.