CF2127H 23 Rises Again

Kiarash 正在采摘草莓带回家…… 如果一个图中每个顶点的度数都不超过 $2$，则称该图为“糖果图”。 给定一个简单、无向且连通的图 $G$，有 $n\le 30$ 个顶点，并且具有如下特殊性质：**每个顶点至多属于 $5$ 个简单环$^{\text{∗}}$**。 你需要求出 $G$ 的所有“糖果”子图$^{\text{†}}$中，最多能有多少条边。 $^{\text{∗}}$简单环是指一个连通子图，其中每个顶点的度数恰好为 $2$。 $^{\text{†}}$图 $G$ 的子图是指其顶点集和边集均为 $G$ 的子集的图。

每个测试点包含多组测试数据。第一行输入测试数据组数 $t$（$1 \le t \le 50$）。接下来是每组测试数据的描述。 每组测试数据的第一行包含两个整数 $n$ 和 $m$（$3 \leq n \leq 30$，$n-1 \leq m \leq \frac{n(n-1)}{2}$），分别表示顶点数和边数。 接下来 $m$ 行，每行两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$），表示第 $i$ 条边连接的两个顶点。 保证给定的图是简单图且连通，并且每个顶点至多属于 $5$ 个简单环。 保证所有测试数据中 $n^2$ 的总和不超过 $900$。

对于每组测试数据，输出一个整数，表示所有“糖果”子图中最多的边数。

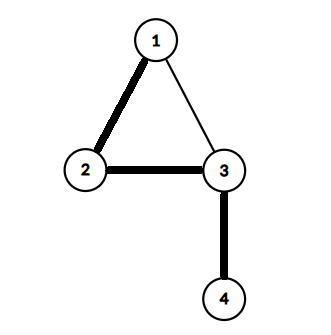
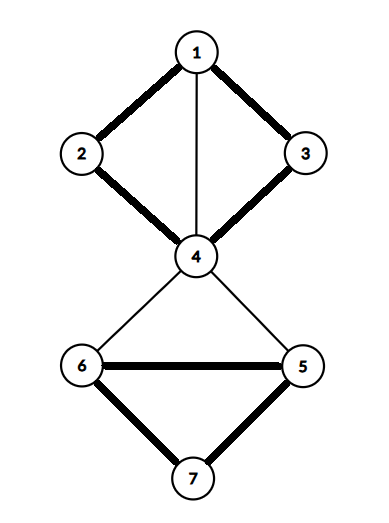
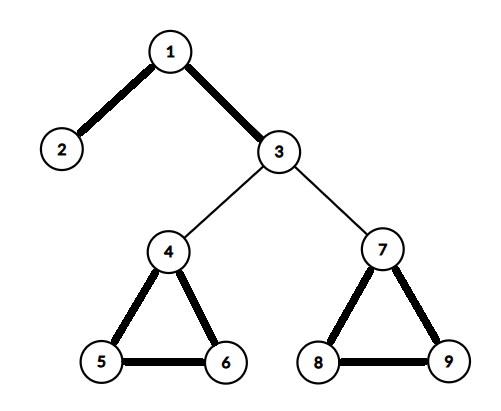
在第一个测试点中，你可以选择下图中标记的边。另一方面，你不能选择所有的边，因为顶点 $3$ 的度数会超过 $2$。所以所有“糖果”子图中最多有 $3$ 条边。  在第二个测试点中，你可以选择下图中标记的边。可以证明，任何“糖果”子图最多有 $7$ 条边。  在第三个测试点中，下图展示了一个边数最多的“糖果”子图。  由 ChatGPT 4.1 翻译