CF2129E Induced Subgraph Queries

给定一个无权无向图 $G$，包含 $n$ 个节点和 $m$ 条边。图 $G$ 中没有自环和重边。 我们用 $V$ 表示 $G$ 的节点集合。对于任意节点子集 $V' \subseteq V$，其对应的诱导子图记作 $G[V']$，定义如下： - $G[V']$ 的节点集合为 $V'$，其边集合为 $G$ 中两个端点都在 $V'$ 内的所有边。 你的任务是回答 $q$ 个询问。每个询问给出三个整数 $l$、$r$ 和 $k$。令 $V' = \{l, l+1, \ldots, r\}$，你需要在 $f(l, G[V'])$、$f(l+1, G[V'])$、$\ldots$、$f(r, G[V'])$ 这 $r-l+1$ 个值中，找出第 $k$ 小的值（即按升序排列后的第 $k$ 个值，重复值按多次计）。 其中，$f(u, G[V']) = \bigoplus_{(u,v)\in G[V']} v$。也就是说，$f(u, G[V'])$ 是 $G[V']$ 中与节点 $u$ 相邻的所有节点编号的按位异或值。 你可以阅读提示部分以便更好地理解题意。

每组测试数据包含多组测试用例。第一行包含一个整数 $t$（$1 \le t \le 1.5 \cdot 10^4$），表示测试用例的数量。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 1.5 \cdot 10^5$，$1 \leq m \leq 1.5 \cdot 10^5$），分别表示节点数和边数。 接下来 $m$ 行，每行两个整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$，$u_i \neq v_i$），表示一条连接 $u_i$ 和 $v_i$ 的无向边。 接下来一行包含一个整数 $q$（$1 \leq q \leq 1.5 \cdot 10^5$），表示询问数量。 接下来的 $q$ 行，每行三个整数 $l$、$r$ 和 $k$（$1 \leq l \leq r \leq n$，$1 \le k \le r-l+1$），表示一次关于诱导子图 $G[\{l, \ldots, r\}]$ 的询问。 保证图中没有自环和重边。 保证所有测试用例中 $n$、$m$、$q$ 的总和分别不超过 $1.5 \cdot 10^5$。

对于每组测试用例，输出 $q$ 个整数，依次表示每个询问的答案。

在第一个测试用例中，输入的图 $G$ 如下图所示。 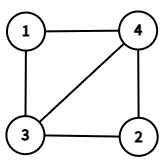 给定的图 $G$。 在第一个询问中，诱导子图 $G[\{1,2\}]$ 如下图所示。可以看到节点 $1$ 和 $2$ 都没有相邻节点，因此 $f(1,G[\{1,2\}])=f(2,G[\{1,2\}])=0$。第 $2$ 小的值为 $0$。 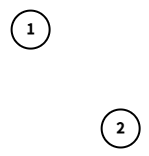 $G[\{1,2\}]$。 在第二个询问中，诱导子图 $G[\{1,2,3\}]$ 如下图所示。可以看到 $f(1,G[\{1,2,3\}])=3$，$f(2,G[\{1,2,3\}])=3$，$f(3,G[\{1,2,3\}])=1 \oplus 2=3$。第 $1$ 小的值为 $3$。 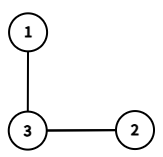 $G[\{1,2,3\}]$。 在第三个询问中，诱导子图 $G[\{2,3,4\}]$ 如下图所示。可以看到 $f(2,G[\{2,3,4\}])=3 \oplus 4=7$，$f(3,G[\{2,3,4\}])=2 \oplus 4=6$，$f(4,G[\{2,3,4\}])=2 \oplus 3=1$。第 $3$ 小的值为 $7$。 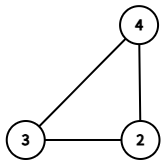 $G[\{2,3,4\}]$。 由 ChatGPT 4.1 翻译