CF2129E Induced Subgraph Queries

You are given an unweighted, undirected graph $ G $ with $ n $ nodes and $ m $ edges. The graph $ G $ contains no self-loops or multiple edges. We denote the node set of $ G $ as $ V $ . For any node subset $ V' \subseteq V $ , the corresponding induced subgraph, denoted by $ G[V'] $ , is defined as follows: - $ G[V'] $ is the graph whose node set is $ V' $ , and whose edge set consists of all edges in $ G $ with both endpoints in $ V' $ . Your task is to answer $ q $ queries. Each query provides three integers $ l $ , $ r $ , and $ k $ . Denoting $ V'=\{l,l+1,\ldots,r\} $ , you need to find the $ k $ -th smallest value among $ f(l,G[V']) $ , $ f(l+1,G[V']) $ , $ \ldots $ , $ f(r,G[V']) $ (i.e., the $ k $ -th value in increasing order; repeated values are counted multiple times). Here, $ f(u,G[V'])=\bigoplus_{(u,v)\in G[V']}v $ . In other words, it is the [bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) value of the labels of all adjacent nodes of node $ u $ in graph $ G[V'] $ . You might want to read the notes for a better understanding.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 1.5 \cdot 10^4 $ ). The description of the test cases follows. Each test case begins with two integers $ n $ and $ m $ ( $ 2 \leq n \leq 1.5 \cdot 10^5 $ , $ 1 \leq m \leq 1.5 \cdot 10^5 $ ) — the number of nodes and edges, respectively. The next $ m $ lines each contain two integers $ u_i $ and $ v_i $ ( $ 1 \leq u_i, v_i \leq n $ , $ u_i \neq v_i $ ), representing an undirected edge between nodes $ u_i $ and $ v_i $ . The next line contains a single integer $ q $ ( $ 1 \leq q \leq 1.5 \cdot 10^5 $ ) — the number of queries. Each of the next $ q $ lines contains three integers $ l $ , $ r $ , and $ k $ ( $ 1 \leq l \leq r \leq n $ , $ 1 \le k \le r-l+1 $ ), defining a query about the induced subgraph $ G[\{l,\ldots,r\}] $ . It is guaranteed that the graph contains no self-loops or multiple edges. It is guaranteed that the sum of $ n $ , $ m $ , and $ q $ over all test cases does not exceed $ 1.5 \cdot 10^5 $ , respectively.

For each test case, output $ q $ integers, representing the answer for each query.

In the first test case, the input graph $ G $ is the one in the following picture. 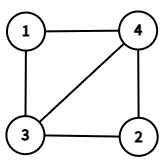 The given graph $ G $ .In the first query, the induced subgraph $ G[\{1,2\}] $ is the one in the following picture. We can see that nodes $ 1 $ and $ 2 $ have no adjacent nodes. Thus, $ f(1,G[\{1,2\}])=f(2,G[\{1,2\}])=0 $ . The $ 2 $ -nd smallest value is $ 0 $ . 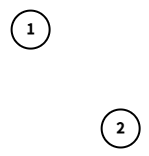 $ G[\{1,2\}] $ .In the second query, the induced subgraph $ G[\{1,2,3\}] $ is the one in the following picture. We can see that $ f(1,G[\{1,2,3\}])=3 $ , $ f(2,G[\{1,2,3\}])=3 $ , and $ f(3,G[\{1,2,3\}])=1 \oplus 2=3 $ . The $ 1 $ -st smallest value is $ 3 $ . 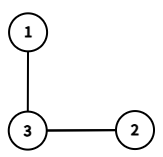 $ G[\{1,2,3\}] $ .In the third query, the induced subgraph $ G[\{2,3,4\}] $ is the one in the following picture. We can see that $ f(2,G[\{2,3,4\}])=3 \oplus 4=7 $ , $ f(3,G[\{2,3,4\}])=2 \oplus 4=6 $ , and $ f(4,G[\{2,3,4\}])=2 \oplus 3=1 $ . The $ 3 $ -rd smallest value is $ 7 $ . 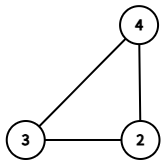 $ G[\{2,3,4\}] $ .