CF2133C The Nether

这是一个交互题。 Steve 最近发现了下界（The Nether），他在自己的世界里建造了 $n$ 个下界传送门，每个传送门的位置都不同。 每个传送门都以有向的方式连接到若干（可能为零）其他传送门。为了避免迷路，Steve 精心设计了传送门网络，使得不存在通过一系列传送门跳跃后又回到原位置的情况；形式上，这个网络构成了一个有向无环图（DAG）。 Steve 不会告诉你哪些传送门彼此相连，但他允许你进行询问。每次询问时，你需要给 Steve 一个位置集合 $S = \{s_1, s_2, \ldots, s_k\}$ 以及一个起始位置 $x \in S$。Steve 会帮你计算从 $x$ 出发，仅经过 $S$ 中的位置的最长路径，并告诉你这条路径包含多少个位置。（如果从 $x$ 出发无法到达 $S$ 中的其他位置，Steve 会回答 $1$。） 你想获得成就“热门旅游胜地”（Hot Tourist Destinations），因此你希望找到一条经过尽可能多位置的路径。Steve 今天格外慷慨，他允许你进行 $2 \cdot n$ 次询问来找到这条路径。

每个测试点包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 每个测试用例的唯一一行包含一个整数 $n$（$2 \le n \le 500$），表示位置的数量。 保证所有测试用例中 $n^3$ 的和不超过 $500^3$。

（交互题，无需输出格式说明。）

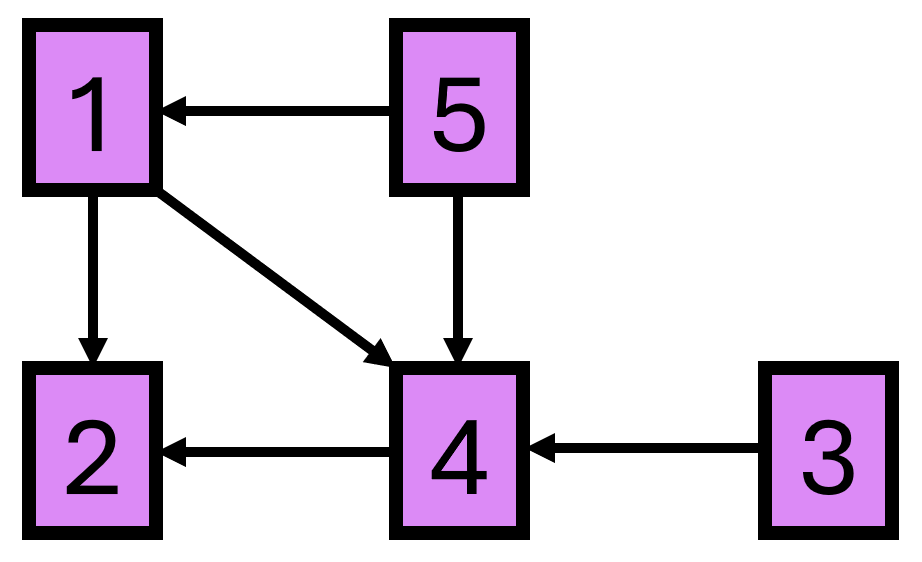
在第一个测试用例中，传送门网络如下图所示：  - 从位置 $1$ 出发，仅经过 $\{1, 2, 3, 4\}$ 的最长路径是 $1 \rightarrow 4 \rightarrow 2$，包含 $3$ 个不同的位置。 - 从位置 $3$ 出发，仅经过 $\{2, 3, 4\}$ 的最长路径是 $3 \rightarrow 4 \rightarrow 2$，包含 $3$ 个不同的位置。 - 从位置 $5$ 出发，仅经过 $\{1, 5\}$ 的最长路径是 $5 \rightarrow 1$，包含 $2$ 个不同的位置。 - 从 $2$ 出发无法到达 $\{2, 4\}$ 中的其他位置，因此 Steve 回答 $1$。 利用这些询问信息，可以确定一条最长路径为 $5 \rightarrow 1 \rightarrow 4 \rightarrow 2$。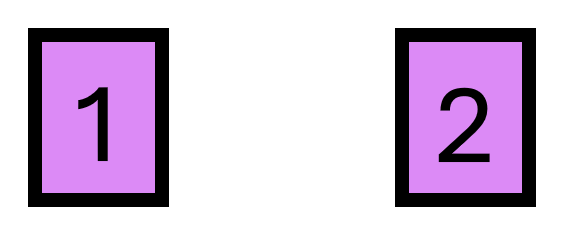 在第二个测试用例中，传送门网络如下图所示：  两个传送门之间没有连接，因此最长路径只包含一个位置。注意 $1\ 2$ 也是一个合法答案。 由 ChatGPT 4.1 翻译