CF2133E I Yearned For The Mines

As a child, Steve yearned for the mines! His mine can be represented as a tree$$$^{\text{∗}}$$$ of $$$n$$$ nodes. Unfortunately, Steve's mine has been infiltrated by his greatest nemesis, Herobrine! At any time, Herobrine is hiding in exactly one node; initially, he may be in any of them. Steve can perform the following operations: - $$$1\,\,x$$$ — Check if Herobrine is currently in node $$$x$$$. If he is, Steve catches him. Otherwise, Herobrine may or may not move to any adjacent node (except the one you just checked). - $$$2\,\,x$$$ — Destroy all edges connected to node $$$x$$$; Herobrine will no longer be able to use them. Afterwards, Herobrine may or may not move to any adjacent node. Find a sequence of at most $$$\left\lfloor \frac{5}{4} \cdot n \right\rfloor$$$ operations that will guarantee Steve catches Herobrine, regardless of Herobrine's initial location and moves. We have a proof that, under the given constraints, this is always possible. $$$^{\text{∗}}$$$A tree is a connected graph without cycles.

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). The description of the test cases follows. The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of nodes. Each of the next $$$n − 1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$), describing an edge between nodes $$$u$$$ and $$$v$$$. It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

For each test case, first output a single integer $$$k$$$ ($$$1 \le k \le \left\lfloor \frac{5}{4} \cdot n \right\rfloor$$$) — the number of operations you wish to perform. Then output $$$k$$$ lines. Line $$$i$$$ ($$$1 \le i \le k$$$) should contain two integers $$$t_i$$$ and $$$x_i$$$ ($$$1 \le t_i \le 2$$$, $$$1 \le x_i \le n$$$), indicating that the $$$i$$$-th operation you wish to perform is operation $$$t_i$$$ on node $$$x_i$$$.

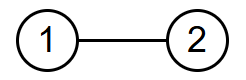
In the first test case, the tree is as follows:  Initially, Herobrine may be in either of the nodes. After the first operation, which checks node $$$1$$$, if Herobrine was in node $$$1$$$, he would be caught, so the only possible node he could be in after the operation is node $$$2$$$ (he cannot move to node $$$1$$$ since it was just checked). Therefore, after the second operation, which checks node $$$2$$$, he must have been caught. 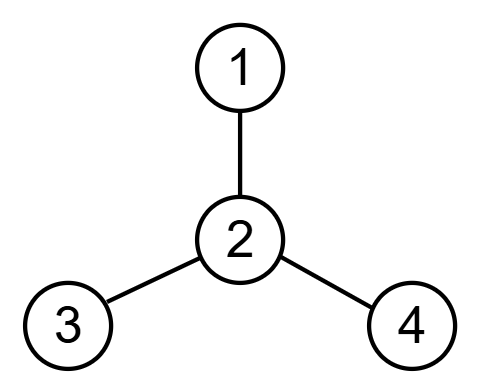In the second test case, the tree is as follows: Initially, Herobrine may be in any of the nodes $$$[1, 2, 3, 4]$$$. After the first operation, Herobrine can only be in nodes $$$[1, 3, 4]$$$. The second operation destroys all edges adjacent to node $$$2$$$. Since all the edges connected to nodes $$$1$$$, $$$3$$$, and $$$4$$$ are now destroyed, Herobrine is unable to move any more no matter where he is located. So after checking those three nodes in operations $$$3$$$, $$$4$$$, and $$$5$$$, he is guaranteed to have been caught.