CF2134D Sliding Tree
题目描述
给定一棵包含 $n$ 个顶点的树(编号从 $1$ 到 $n$)。你可以按如下多步操作(称为滑动操作)来修改其结构:
1. 选择三个不同的顶点 $a$、$b$、$c$,其中 $b$ 直接和 $a$、$c$ 相连。
2. 对于 $b$ 的所有邻居 $d$(不包括 $a$ 和 $c$),移除 $b$ 和 $d$ 之间的边,并将 $d$ 直接与 $c$ 相连。
例如,下图展示了在最左侧的树中,$a = 4$,$b = 3$,$c = 5$ 时的这一操作。
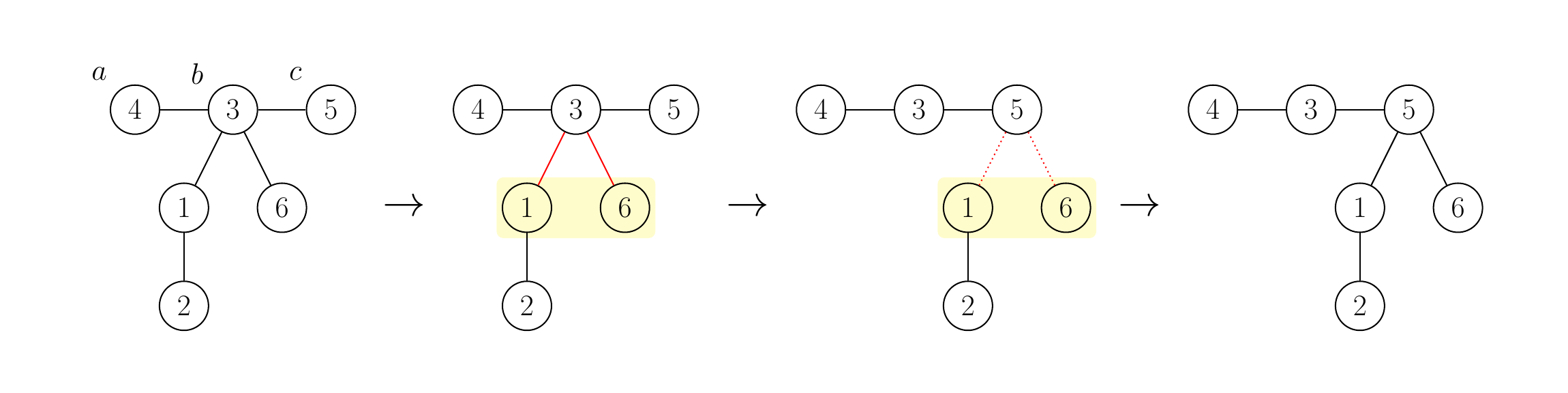
可以证明,经过一次滑动操作后,得到的图仍然是一棵树。
你的任务是找到一系列滑动操作,使树最终转变为一条路径图,并且操作次数最少。如果至少需要一次操作,则只需输出最优方案中的第一次滑动操作。可以证明,一定可以用有限步操作将树变为一条路径图。
注:
$^{\ast}$ 一棵树是一个无环连通图。
$^{\dagger}$ 路径图是每个顶点的度数都不超过 $2$ 的树。注意,只有一个顶点且没有边的图也算作路径图。
输入格式
每组测试数据包含多组测试用例。
第一行为测试用例个数 $t$($1 \le t \le 10^4$)。每组测试用例描述如下:
第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^5$),表示树的顶点数。
接下来 $n-1$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示树中的一条边。
保证给定的边能构成一棵树。
保证所有测试用例的 $n$ 之和不超过 $2 \times 10^5$。
输出格式
对于每个测试用例:
- 如果不需要任何操作(即输入树本身就是一条路径图),输出 $-1$。
- 否则,输出第一次滑动操作选择的三个不同顶点 $a$、$b$、$c$($1 \le a, b, c \le n$)。
如果存在多种合法的第一次操作,你可以输出其中任意一种。
说明/提示
第一个测试用例与题面例图一致。可以证明,无法在少于 2 次操作内将给定树变为路径图。
然而,可以通过如下两次操作将树变为路径图:首先按题面例图以 $a=4$、$b=3$、$c=5$ 操作;接着,使用 $a=3$、$b=5$、$c=6$ 进行操作。操作后,树变为一条路径图。第二次操作如下图所示:
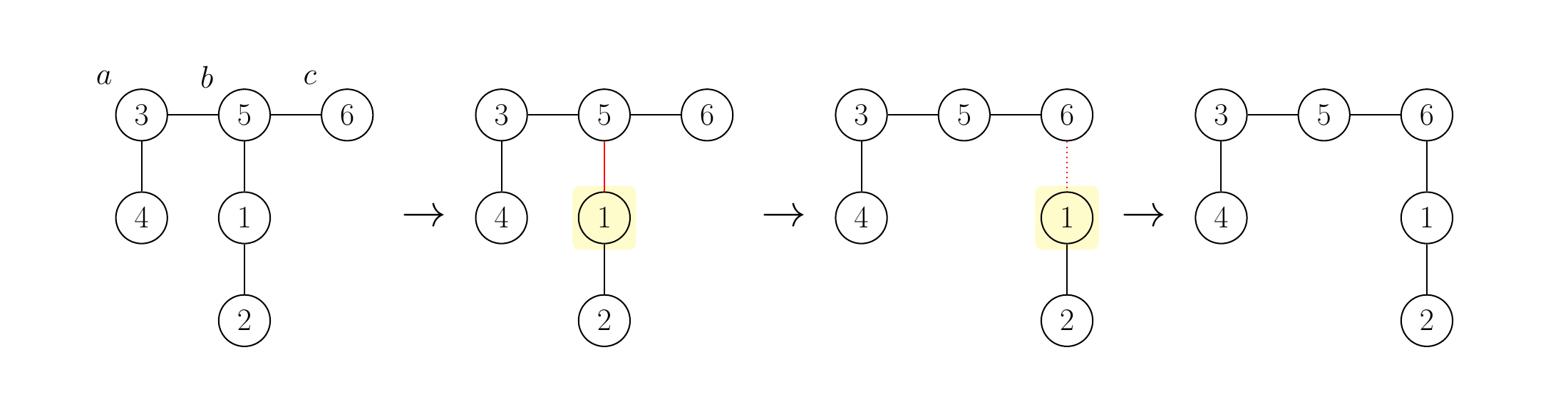
因此,可以得到最小次数的滑动操作序列。注意,只需输出第一次操作;不需要输出操作次数或后续操作。
在第二个和第三个测试点中,输入的树本身已经是一条路径图,因此不需要任何操作。
由 ChatGPT 5 翻译