CF2138C2 Maple and Tree Beauty (Hard Version)

Maple 拥有一棵有根树，这棵树有 $n$ 个顶点，编号为 $1$ 到 $n$，其中根节点编号为 $1$。树中的每个顶点都被标记为 $0$ 或 $1$。不幸的是，Maple 忘记了这些顶点的标记，只记得树中恰好有 $k$ 个顶点被标记为 $0$，$n - k$ 个顶点被标记为 $1$。 对每个顶点，我们将其“名字”定义为从根节点到该顶点路径上所有顶点标记串联而成的二进制字符串。更正式地说，$\text{name}_1 = \text{label}_1$，对于 $2 \le u \le n$，$\text{name}_u = \text{name}_{p_u} + \text{label}_u$，其中 $p_u$ 是顶点 $u$ 的父节点，$+$ 表示字符串拼接。 树的“美丽值”定义为所有**叶子节点**的名字的最长公共子序列的长度。 你的任务是，在所有有 $k$ 个 $0$ 和 $n-k$ 个 $1$ 的标记方案中，计算该树的最大美丽值。 注： $^*$ 一个序列 $a$ 是序列 $b$ 的子序列，若 $a$ 可以通过删除 $b$ 的若干（可以为零或全部）元素而得到。最长公共子序列指能同时成为所有字符串 $s_1, s_2, \ldots, s_m$ 的子序列的最长字符串。 $^\dagger$ 叶子节点指的是没有子节点的顶点。

本题包含多组测试用例。第一行包含整数 $t$（$1 \leq t \leq 10^4$），表示测试用例数量。 每个测试用例的第一行包含两个整数 $n$ 和 $k$（$2 \leq n \leq 2 \cdot 10^5$，$0 \leq k \leq n$），分别表示顶点数和被标记为 $0$ 的顶点数。 第二行包含 $n - 1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \leq p_i \leq i - 1$），表示第 $i$ 个顶点的父节点编号。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示该树所有标记方案中最大美丽值。

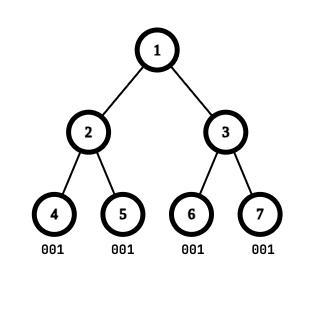
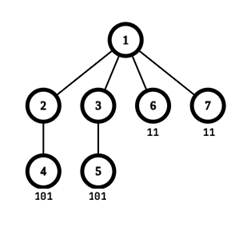
 在第一个测试用例中，最大美丽值为 $3$，当顶点标记为 $[0, 0, 0, 1, 1, 1, 1]$ 时，最长公共子序列为 001。  在第二个测试用例中，最大美丽值为 $2$，当顶点标记为 $[1, 0, 0, 1, 1, 1, 1]$ 时，最长公共子序列为 11。 由 ChatGPT 5 翻译