CF2138D Antiamuny and Slider Movement

Antiamuny 正在管理 $n$ 个滑块，这些滑块在一个长度为 $m$ 的一维轨道上。每个滑块正好占用一个单位长度，并且初始时位于不同的位置。滑块从左到右编号为 $1$ 到 $n$，第 $i$ 个滑块初始时位于位置 $a_i$。 现在有 $q$ 次操作。每次操作由两个整数 $i,x$ 描述（$1 \leq i \leq n$，且 $i \leq x \leq m-n+i$）。该操作将第 $i$ 个滑块移动到位置 $x$。然而，如果这个操作会导致与其他滑块发生碰撞（也就是在第 $i$ 个滑块当前位置和目标 $x$ 之间存在其他滑块），那么这些阻碍滑块会被按相同方向依次推进一格，直到不再发生碰撞，这可能引发连锁反应（即一个滑块推着另一个滑块移动），直到所有滑块都再次占据不同的位置。 请注意，这些操作不会改变滑块的相对顺序：第 $i$ 个滑块始终是从左到右的第 $i$ 个滑块。此外，$x$ 的约束保证所有滑块位置始终在 $1$ 到 $m$ 之间，不会出界。 例如，假设初始滑块位置为 $[1,3,5,7,9]$。如果将第 $5$ 个滑块（位于 $9$）移动到 $6$ 号位置，它会推动第 $4$ 个滑块从 $7$ 移动到 $5$，进一步推动第 $3$ 个滑块从 $5$ 移动到 $4$。最后滑块的位置为 $[1,3,\textbf{4},\textbf{5},\textbf{6}]$。 不幸的是，Antiamuny 忘记了 $q$ 次操作的应用顺序。为恢复所有结果，他决定独立模拟这 $q!$ 种操作顺序的所有排列。对于每一个长度为 $q$ 的排列 $p$，定义 $f_i(p)$ 表示在按 $p$ 的顺序执行所有操作后，第 $i$ 个滑块的最终位置。 换句话说，从初始位置 $a_1,a_2,\ldots,a_n$ 出发，先执行 $p_1$ 指定的操作、再执行 $p_2$ 指定的操作，依次至 $p_q$ 指定的操作。$f_i(p)$ 为这一过程中第 $i$ 个滑块的最后位置。 你的任务是，对于每个滑块 $i$（$1 \le i \le n$），计算所有 $q!$ 种操作顺序下 $f_i(p)$ 的和。由于结果可能很大，请将每个答案对 $10^9+7$ 取模后输出。 $^*$一个长度为 $q$ 的排列是由 $1$ 到 $q$ 的 $q$ 个不同整数组成的数组，顺序任意。例如，$[2,3,1,5,4]$ 是一个排列，$[1,2,2]$ 不是（$2$ 出现了两次），$[1,3,4]$ 也不是（$q=3$ 但有 $4$）。

每组测试包含多组数据。第一行输入测试组数 $t$（$1 \le t \le 10^3$）。 每组测试数据的第一行为三个整数 $n$、$m$、$q$（$1 \leq n,q \leq 5\times 10^3$，$n \leq m \leq 10^9$），代表滑块数量、轨道长度和操作数量。 第二行输入 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \leq a_1 < a_2 < \ldots < a_n \leq m$），分别为初始时每个滑块的位置。 接下来 $q$ 行，每行两个整数 $i,x$（$1 \leq i \leq n$, $i \leq x \leq m-n+i$），分别表示要移动的滑块编号，以及目标位置。 保证所有测试数据的 $n$ 和 $q$ 之和不超过 $5\times 10^3$。

对于每组测试数据，输出 $n$ 个整数，第 $i$ 个整数为所有 $q!$ 种操作顺序下，第 $i$ 个滑块的最终位置之和 $f_i(p)$ 的和，对 $10^9+7$ 取模。

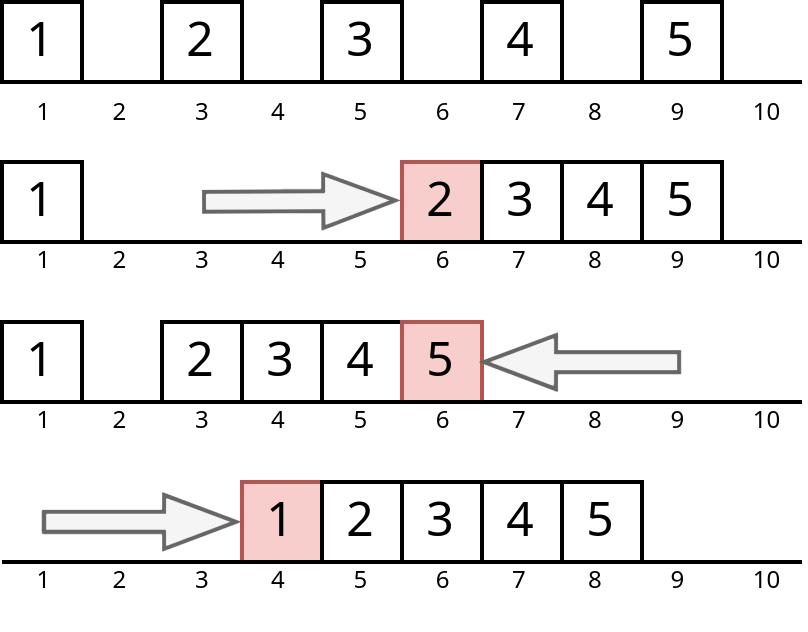
在第一个测试点中： - 若操作顺序为 $[2,1,3]$，那么先执行第 $2$ 个操作，将第 $2$ 个滑块移动到位置 $6$；再进行第 $1$ 个操作，将第 $5$ 个滑块移动到位置 $6$；最后进行第 $3$ 个操作，将第 $1$ 个滑块移动到位置 $4$。每次操作后滑块的位置见下图。最终滑块的位置为 $[4,5,6,7,8]$。  - 若顺序为 $[1,2,3]$，最终滑块位置为 $[4,6,7,8,9]$。 - 若顺序为 $[1,3,2]$，最终滑块位置为 $[4,6,7,8,9]$。 - 若顺序为 $[2,3,1]$，最终滑块位置为 $[2,3,4,5,6]$。 - 若顺序为 $[3,1,2]$，最终滑块位置为 $[2,6,7,8,9]$。 - 若顺序为 $[3,2,1]$，最终滑块位置为 $[2,3,4,5,6]$。 对于第 $1$ 个滑块，所有 $6$ 种情况的位置和为 $4+4+4+2+2+2=18$。 对于第 $2$ 个滑块，所有 $6$ 种情况的位置和为 $5+6+6+3+6+3=29$。 对于第 $3$ 个滑块，所有 $6$ 种情况的位置和为 $6+7+7+4+7+4=35$。 对于第 $4$ 个滑块，所有 $6$ 种情况的位置和为 $7+8+8+5+8+5=41$。 对于第 $5$ 个滑块，所有 $6$ 种情况的位置和为 $8+9+9+6+9+6=47$。 由 ChatGPT 5 翻译