CF2138F Ode to the Bridge Builder

给你一个二维平面。初始时，两个点 $P_1$ 和 $P_2$ 分别位于 $(0,0)$ 和 $(1,0)$，并且两点间有一条线段连接。你可以通过如下操作绘制三角形： - 选择两个由线段直接连接的点 $A$ 和 $B$（即 $A$ 和 $B$ 必须是已存在线段的两端点）。 - 选择两个实数 $x$ 和 $y$，满足 $-2\cdot 10^4 \le x, y \le 2\cdot 10^4$。在坐标 $(x,y)$ 处绘制一个新点 $C$。然后，绘制线段 $AC$ 和 $BC$，从而构成三角形 $\triangle ABC$。 - 新三角形 $\triangle ABC$ 的每条边的长度 $l$ 都必须满足 $0.5\le l\le 1$。 注意，每次操作只绘制一个新点和两条新线段。 你的任务是，使用至多 $m = \left\lceil 2\sqrt{p^2 + q^2}\right\rceil$ 次操作，在坐标 $(p, q)$ 处绘制一个点，其中 $\lceil x\rceil$ 表示大于等于 $x$ 的最小整数。保证 $p$ 和 $q$ 都是正整数。 由于可能存在精度误差： - 构造出的顶点只需距离 $(p,q)$ 不超过 $10^{-4}$。 - 对于三角形的边长，允许绝对误差 $10^{-8}$（即 $0.5 - 10^{-8} \le l \le 1 + 10^{-8}$）。 注意，目标点可以在最后一次操作之前就已经被创建（见第二个测试用例）。

每个测试包含多组测试用例。第一行包含测试用例数 $t$（$1 \le t \le 1000$）。接下来是各个测试用例的描述。 每个测试用例第一行包含三个整数 $p, q$ 和 $m$（$1 \le p, q \le 10^4$，$m = \left\lceil 2\sqrt{p^2 + q^2}\right\rceil$）——即目标点的 $x$ 和 $y$ 坐标，以及最多允许执行的操作数。 保证所有测试用例中 $m$ 的总和不超过 $10^5$。

对于每个测试用例，输出一个整数 $n$（$0\le n \le m$），表示实际使用的操作数。 随后输出 $n$ 行，每行描述一次操作。第 $i$ 次操作输出四个值：两个整数 $u, v$（$1 \le u,v\le i+1$, $u\neq v$），表示选中的两点的编号；随后两个实数 $x$ 和 $y$（$-2\cdot 10^4\le x, y \le 2\cdot 10^4$），表示新点的坐标。 编号分配规则如下： - 点 $P_1(0,0)$ 和 $P_2(1,0)$ 的编号分别为 $1$ 和 $2$。 - 第 $j$ 次操作绘制的新点编号为 $j+2$。 如果存在多种在 $m$ 次操作内到达目标点的有效方案，你可以输出任意一种。

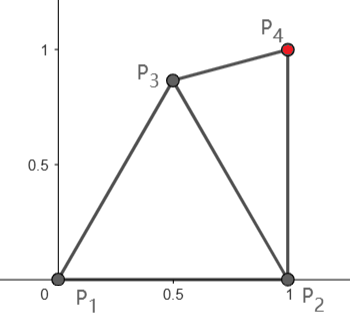
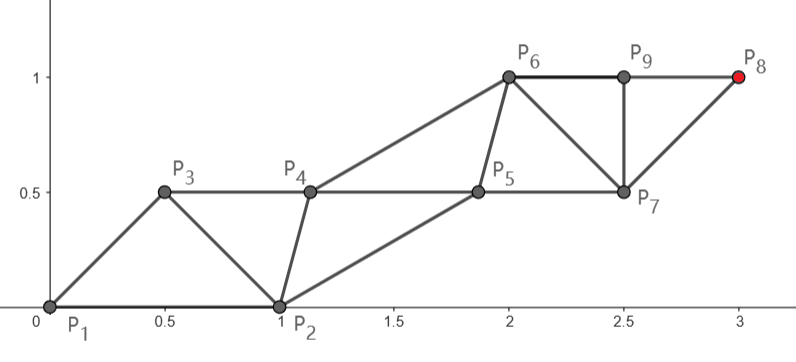
在第一个样例中，最多可进行 $\lceil 2\sqrt{2}\rceil=3$ 次操作，下面的方案只用了两步： 1. 选择点 $A = P_1$ 和 $B = P_2$，在 $\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)$ 处绘制新点 $P_3$。此时三角形 $\triangle P_1P_2P_3$ 的三边均为 $1$。 2. 选择 $A = P_2$，$B = P_3$，在 $(1, 1)$ 处绘制新点 $P_4$，此时 $\triangle P_2P_3P_4$ 中 $|P_2P_3|=|P_2P_4|=1$，$|P_3P_4|=2\sin(15^\circ)\approx0.5176\ge 0.5$。  在第二个样例中，最多可进行 $\left\lceil 2\sqrt{10}\right\rceil=7$ 次操作。 如下图方案中，点 $P_4$ 和 $P_5$ 的坐标分别为 $\left(2-\frac{\sqrt{3}}{2},\frac{1}{2}\right)$ 和 $\left(1+\frac{\sqrt{3}}{2},\frac{1}{2}\right)$，且 $|P_4P_6|=|P_2P_5|=1$。可以验证所有线段的长度均在 $[0.5,1]$ 范围内。 注意，最后一次操作其实可以省略，删除最后一步方案依然正确。  由 ChatGPT 5 翻译