CF2147A Shortest Increasing Path

You are at $ (0, 0) $ in a rectangular grid and want to go to $ (x, y) $ . In order to do so, you are allowed to perform a sequence of steps. Each step consists of moving a positive integer amount of length in the positive direction of either the $ x $ or the $ y $ axis. The first step must be along the $ x $ axis, the second along the $ y $ axis, the third along the $ x $ axis, and so on. Formally, if we number steps from one in the order they are done, then odd-numbered steps must be along the $ x $ axis and even-numbered steps must be along the $ y $ axis. Additionally, each step must have a length strictly greater than the length of the previous one. Output the minimum number of steps needed to reach $ (x, y) $ , or $ -1 $ if it is impossible.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first and only line of each case contains two integers $ x $ and $ y $ ( $ 1 \le x, y \le 10^9 $ ).

For each test case, output the minimum number of steps to reach $ (x, y) $ or $ -1 $ if it is impossible.

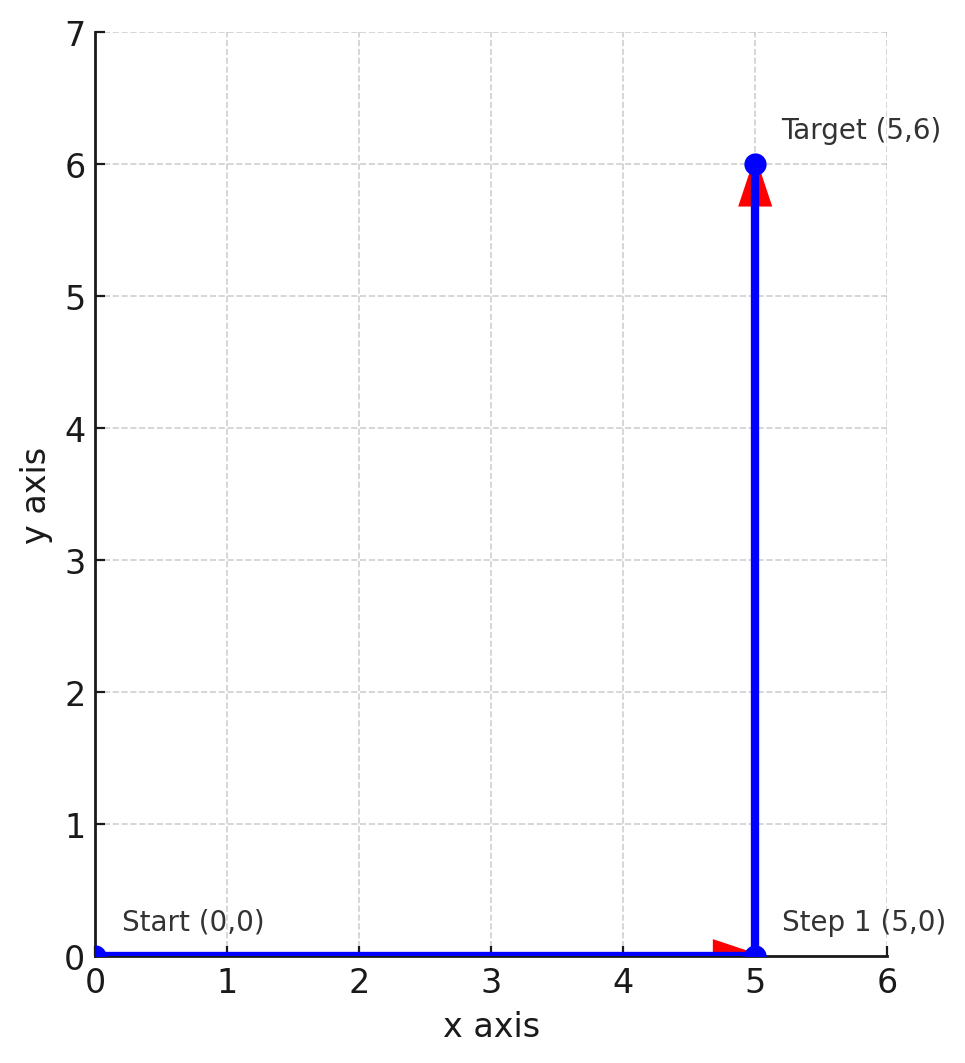
[Visualizer link](https://codeforces.com/assets/contests/2147/A_cdXXtjqxZBm9unXAJx2Q.html) In the second test case, you can move to $ (5, 0) $ by moving $ 5 $ along the $ x $ axis and then to $ (5, 6) $ by moving $ 6 $ along the $ y $ axis.  In the third test case, you can move to $ (1, 0) $ , then to $ (1, 2) $ , and finally to $ (4, 2) $ . 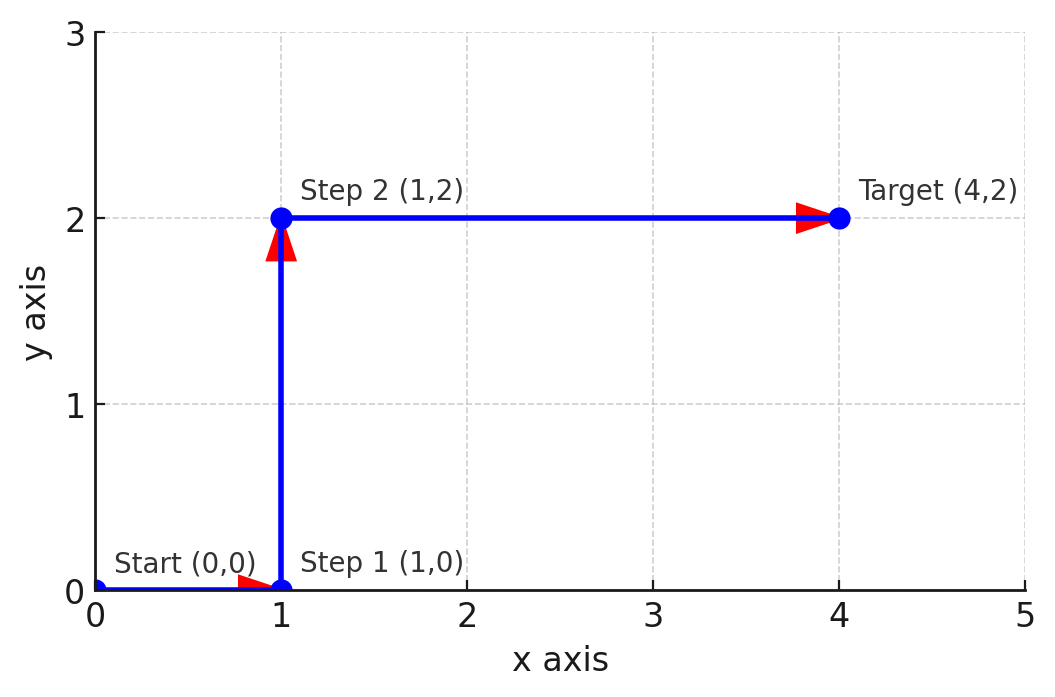 In the fourth test case, reaching $ (1, 1) $ is impossible since after moving to $ (1, 0) $ along the $ x $ axis, you are forced to move at least $ 2 $ along the $ y $ axis.