CF2148B Lasers

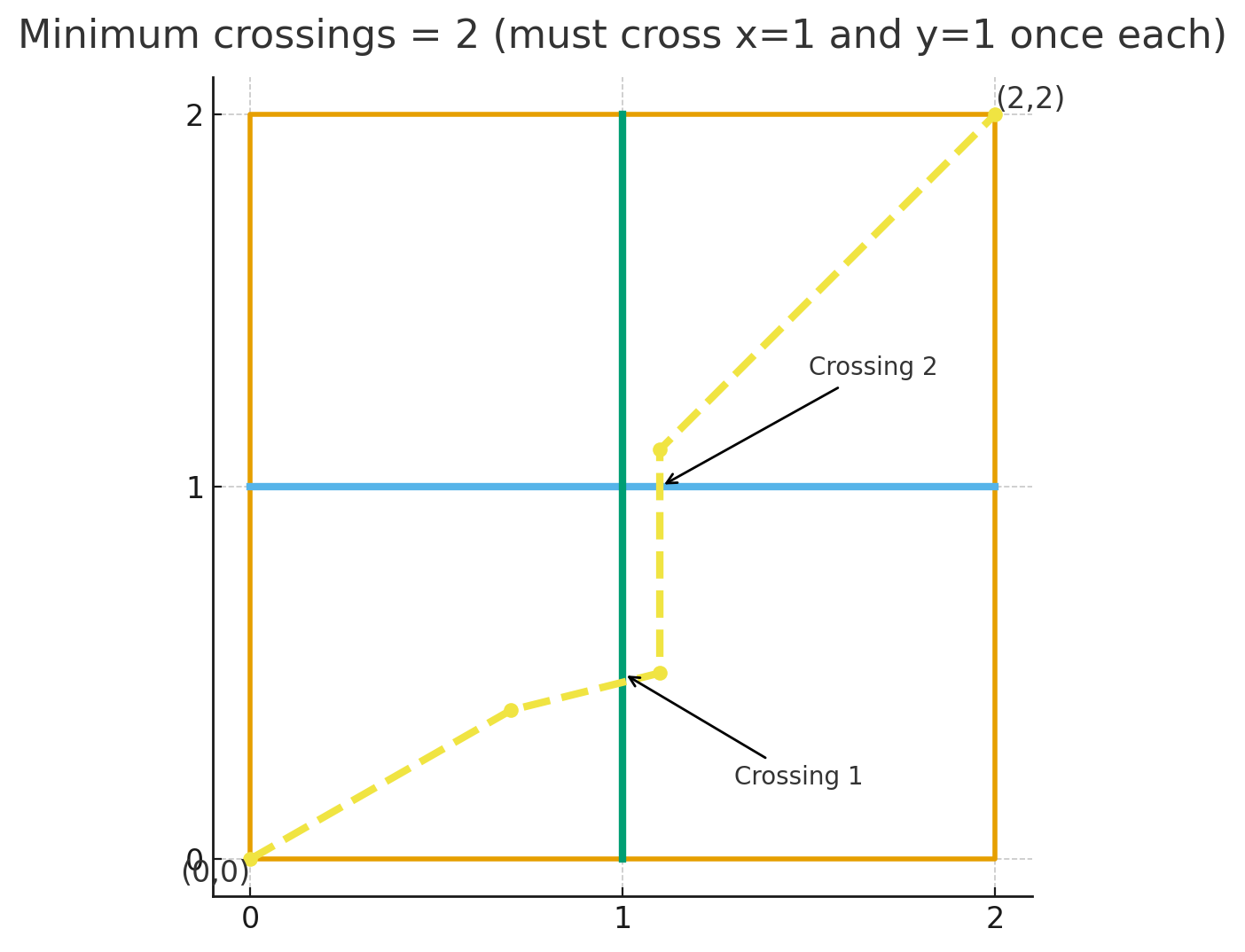
在一个二维坐标平面上，坐标范围为 $$(0,0)$$ 到 $$(x, y)$$。你位于 $$(0,0)$$，目标是到达 $$(x, y)$$。 但是，平面上有 $n$ 条水平激光，第 $i$ 条激光从 $$(0, a_i)$$ 到 $$(x, a_i)$$，还存在 $m$ 条竖直激光，第 $i$ 条激光从 $$(b_i, 0)$$ 到 $$(b_i, y)$$。 你可以沿任意方向移动以到达 $$(x, y)$$，但你的运动轨迹必须是平面内的一条连续曲线。每当你穿越一条水平或一条竖直激光，计为一次穿越。特别地，如果你经过两条激光的交点，则计为两次穿越。 例如，若 $x = y = 2$，$n = m = 1$，$a = [1]$，$b = [1]$，运动方式如下所示：  问最少需要穿越多少次激光才能到达 $$(x, y)$$。

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例数量。 每组测试数据的第一行包含四个整数 $n$、$m$、$x$ 和 $y$（$1 \leq n, m \leq 2 \times 10^5,\ 2 \leq x ,y \leq 10^9$）。 接下来一行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$0 < a_i < y$），表示所有水平激光的 $y$ 坐标。保证对于所有 $i > 1$，有 $a_i > a_{i-1}$。 接下来一行包含 $m$ 个整数 $b_1, b_2, \ldots, b_m$（$0 < b_i < x$），表示所有竖直激光的 $x$ 坐标。保证对于所有 $i > 1$，有 $b_i > b_{i-1}$。 保证所有测试用例的 $n$ 和 $m$ 之和不超过 $2 \times 10^5$。

对于每组测试数据，输出到达 $$(x, y)$$ 所需穿越激光的最小次数。

由 ChatGPT 5 翻译