CF2148B Lasers

There is a 2D-coordinate plane that ranges from $ (0,0) $ to $ (x, y) $ . You are located at $ (0,0) $ and want to head to $ (x, y) $ . However, there are $ n $ horizontal lasers, with the $ i $ -th laser continuously spanning $ (0, a_i) $ to $ (x, a_i) $ . Additionally, there are also $ m $ vertical lasers, with the $ i $ -th laser continuously spanning $ (b_i, 0) $ to $ (b_i, y) $ . You may move in any direction to reach $ (x, y) $ , but your movement must be a continuous curve that lies inside the plane. Every time you cross a vertical or a horizontal laser, it counts as one crossing. Particularly, if you pass through an intersection point between two lasers, it counts as two crossings. 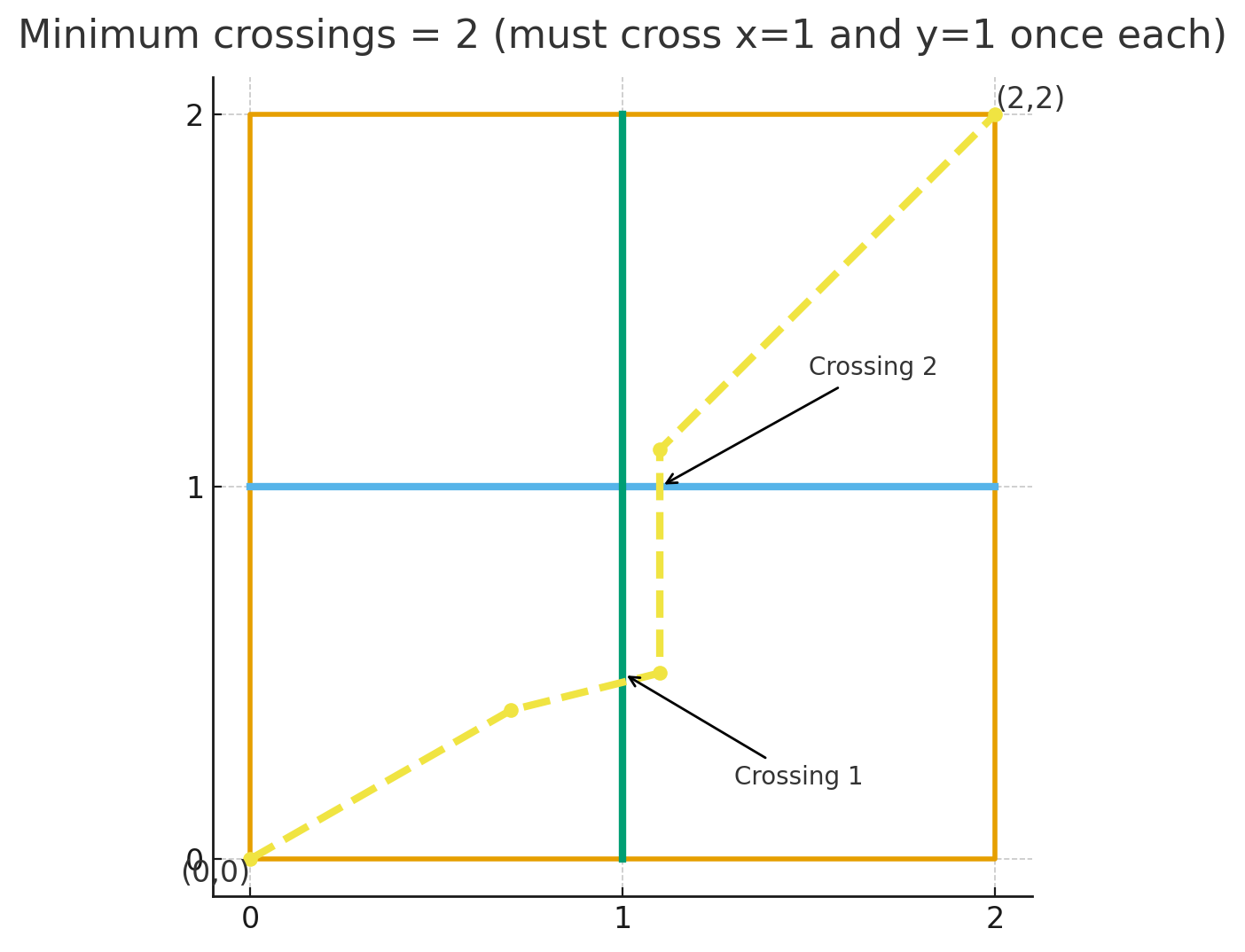For example, if $ x = y = 2 $ , $ n = m = 1 $ , $ a = [1] $ , $ b = [1] $ , the movement can be as follows: What is the minimum number of crossings necessary to reach $ (x, y) $ ?

The first line contains $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The first line of each test case contains four integers $ n $ , $ m $ , $ x $ , and $ y $ ( $ 1 \leq n, m \leq 2 \cdot 10^5, 2 \leq x ,y \leq 10^9 $ ). The following line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 0 < a_i < y $ ) — the y-coordinates of the horizontal lasers. It is guaranteed that $ a_i > a_{i-1} $ for all $ i > 1 $ . The following line contains $ m $ integers $ b_1, b_2, \ldots, b_m $ ( $ 0 < b_i < x $ ) — the x-coordinates of the vertical lasers. It is guaranteed that $ b_i > b_{i-1} $ for all $ i > 1 $ . It is guaranteed that the sum of $ n $ and $ m $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output the minimum number of crossings necessary to reach $ (x, y) $ .