CF2152B Catching the Krug

Doran 和 Krug 正在一个由 $(n + 1) \times (n + 1)$ 个格子组成的网格上玩游戏，网格上的每个单元格坐标是从 $0$ 到 $n$（包含 $0$ 和 $n$）的整数对。Krug 的目标是尽可能长时间不被 Doran 抓住，而 Doran 的目标是尽快抓住 Krug。当 Doran 和 Krug 站在同一个格子上时，称 Doran 抓住了 Krug。 游戏规则如下，Krug 和 Doran 轮流行动，Krug 先手： - Krug 可以选择留在原地，或者移动到上下左右相邻的格子（不可斜向移动）。具体而言，如果 Krug 当前在 $(a, b)$，她可以留在 $(a, b)$，或移动到 $(a-1, b), (a, b-1), (a, b+1), (a+1, b)$。 - Doran 可以选择留在原地，或者移动到上下左右或斜向相邻的格子。具体而言，如果 Doran 当前在 $(c, d)$，他可以留在 $(c, d)$，或移动到 $(c-1, d-1), (c-1, d), (c-1, d+1), (c, d-1), (c, d+1), (c+1, d-1), (c+1, d), (c+1, d+1)$。 - 两名玩家都不能走出网格。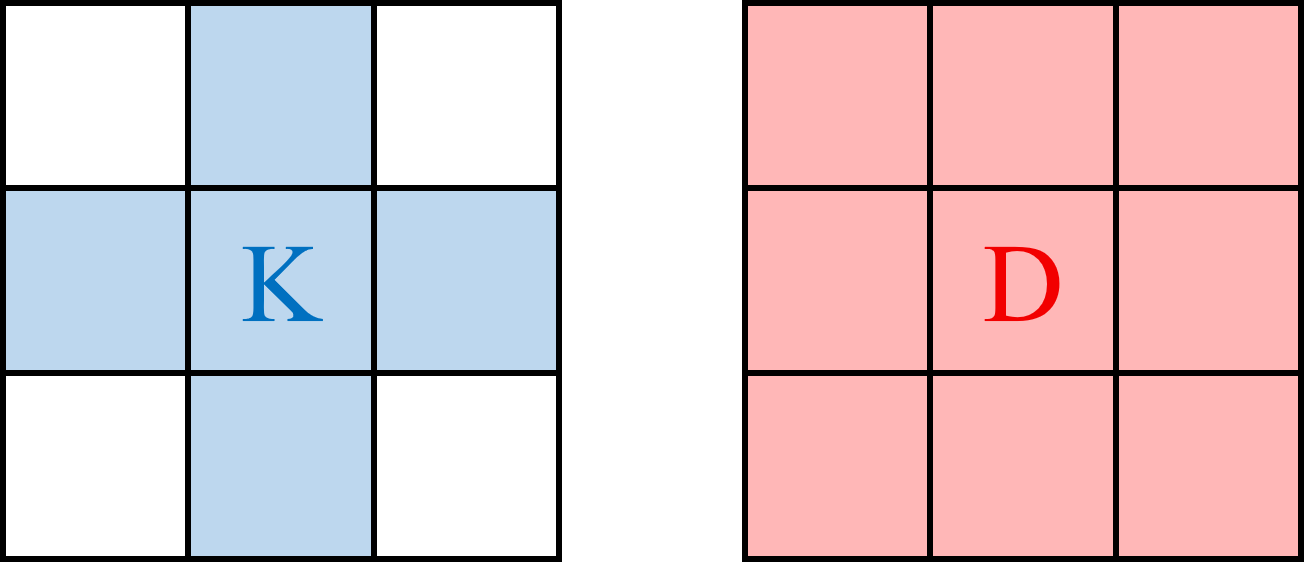  如上图，分别展示了 Krug 和 Doran 的可行动位置。字母 'K' 和 'D' 分别代表 Krug 和 Doran 的当前位置，色块表示在各自回合可能到达的位置。 Krug 的存活时间定义为在双方的最优策略下，从初始位置开始直到 Doran 抓住 Krug 之前，经历了多少次 Doran 的回合。如果 Krug 可以无限存活，则输出 $-1$。

每个测试包含多个测试用例。第一行输入测试用例数量 $t$，$(1 \le t \le 10^4)$。接下来 $t$ 行，每行输入五个整数 $n$, $r_K$, $c_K$, $r_D$, $c_D$，$(1 \le n \le 10^9, 0 \le r_K, c_K, r_D, c_D \le n, (r_K, c_K) \ne (r_D, c_D))$，其中 $n$ 表示网格的大小，$(r_K, c_K)$ 表示 Krug 的起始格子，$(r_D, c_D)$ 表示 Doran 的起始格子。

对于每个测试用例，当双方都采取最优策略时，输出 Krug 的存活时间。如果 Krug 可以无限存活，输出 $-1$。

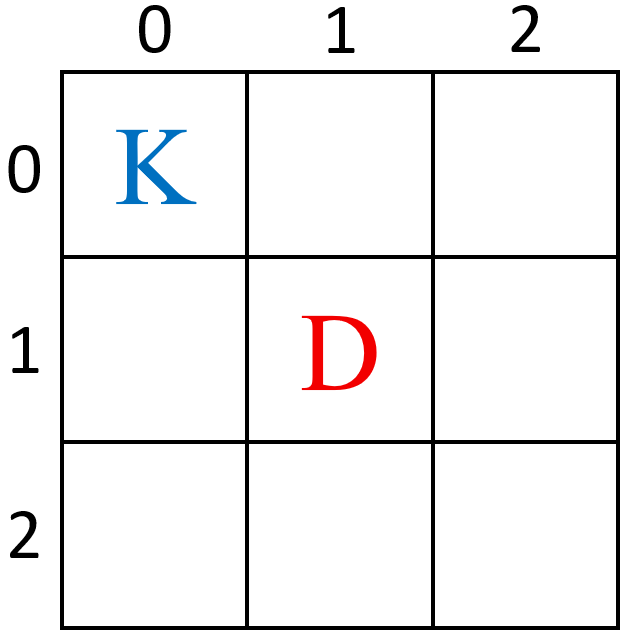
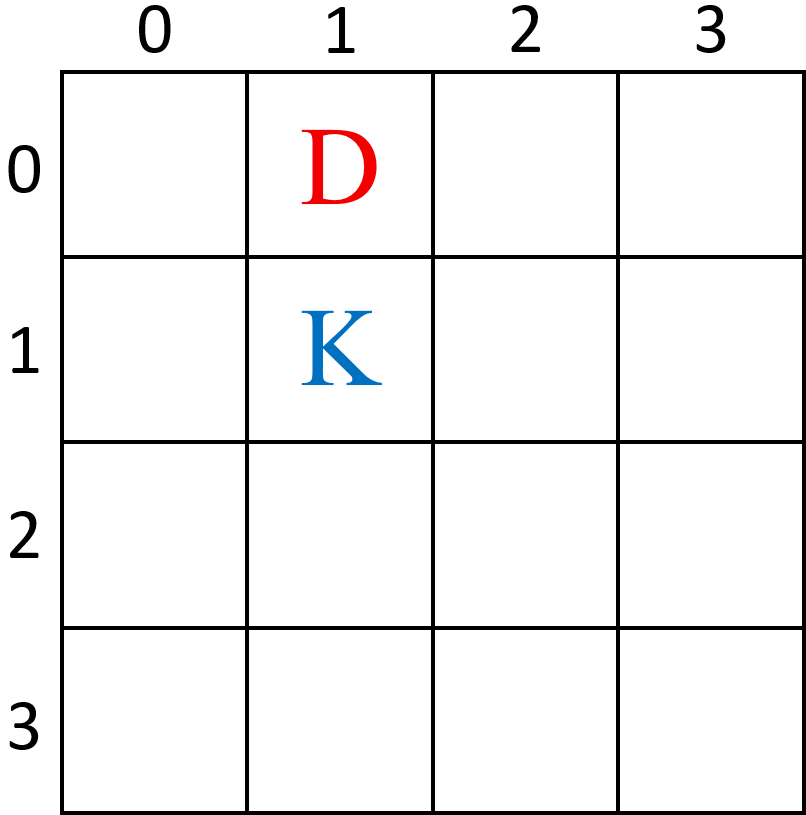
第一个样例说明： Krug 初始在 $(0,0)$，Doran 初始在 $(1,1)$。Krug 回合可移动到 $(0,0)$、$(0,1)$ 或 $(1,0)$。 Doran 从 $(1,1)$ 出发，在 $3 \times 3$ 网格范围内任意移动一次即可到达任意格子，因此无论 Krug 如何走，Doran 都能在他第一次回合就抓到 Krug。Krug 的存活时间为 $1$。  第二个样例说明： Krug 初始在 $(1,1)$，Doran 在 $(0,1)$。为了在 Doran 的第一次回合幸存，Krug 必须走到 Doran 无法一步到达的位置，即 $(2,1)$。 Krug 走到 $(2,1)$ 后，Doran 向 $(1,1)$ 靠近。 接下来第二回合 Krug 又要走到 Doran 无法一步到达的位置，也就是 $(3,1)$，Doran 接着到 $(2,1)$。 此时第三回合 Krug 无论如何移动，Doran 下回合都能追上她。最优策略下 Krug 的存活时间为 $3$。  由 ChatGPT 5 翻译