CF2152G Query Jungle

Oner 是一名打野选手——他的职责是在“丛林”中狩猎怪物。鉴于他在丛林中看到的树的数量，他对树上查询类问题情有独钟。 给定一棵 $n$ 个结点的树，树以 $1$ 号结点为根。每个结点可能包含怪物，也可能不包含怪物。 你需要找到最小的整数 $k$，使得存在 $k$ 条路径，满足以下条件： - 每条路径必须从根（顶点 $1$）开始。 - 树上每个包含怪物的结点，必须在至少一条路径中出现。一个结点若在路径的任一端点或路径上的任何一个点上都算被“包含”。 为了增添难度，你还要回答 $q$ 个查询。每个查询给定一个顶点 $v$，对于 $v$ 的子树内的每个结点，其状态会“反转”：原本有怪物的变为没有怪物，原本没有怪物的变为有怪物。每次查询后，你需要再次解决原问题，即输出更新后树的最小路径数。 注意查询具有累积性，所以每次查询的影响会影响之后所有的查询。

每份测试数据包含多组测试用例。第一行为整数 $t$（$1 \le t \le 20\,000$），表示用例数。以下为每组测试用例的描述。 第一行包含一个整数 $n$（$2 \le n \le 250\,000$），表示树的结点数量。 接下来的 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$a_i \in \{0, 1\}$）：如果 $a_i = 1$，则 $i$ 号顶点有怪物；否则没有怪物。 接下来 $n-1$ 行，每行两个整数 $u$ 和 $v$（$1 \le u, v \le n, u \ne v$），表示树中的一条边。保证这些边构成一棵树。 之后一行包含一个整数 $q$（$0 \le q \le 250\,000$）——查询数。 接下来的 $q$ 行，每行一个整数 $v_i$（$1 \le v_i \le n$），表示第 $i$ 次查询的位置。 保证所有测试用例的 $n$ 之和不超过 $250\,000$，所有 $q$ 之和也不超过 $250\,000$。

输出 $q+1$ 行。第一行为初始状态下所需最小路径数 $k$。之后每行输出每次查询后的答案。

测试用例 1： 初始状态：怪物在顶点 $\{2, 4, 5\}$。我们需要两条路径：$1 \to 7 \to 3 \to 2$ 和 $1 \to 7 \to 5 \to 4$。答案为 $2$。 第一次查询后（$v=2$）：怪物在顶点 $\{4, 5\}$。仅需一条路径 $1 \to 7 \to 5 \to 4$。答案为 $1$。 第二次查询后（$v=4$）：怪物在顶点 $\{5\}$。仅需一条路径 $1 \to 7 \to 5$。答案为 $1$。 第三次查询后（$v=6$）：怪物在顶点 $\{5, 6\}$。需要两条路径：$1 \to 7 \to 5$ 和 $1 \to 6$。答案为 $2$。 第四次查询后（$v=7$）：怪物在顶点 $\{2, 3, 4, 6, 7\}$。需要三条路径：$1 \to 6$，$1 \to 7 \to 5 \to 4$，和 $1 \to 7 \to 3 \to 2$。答案为 $3$。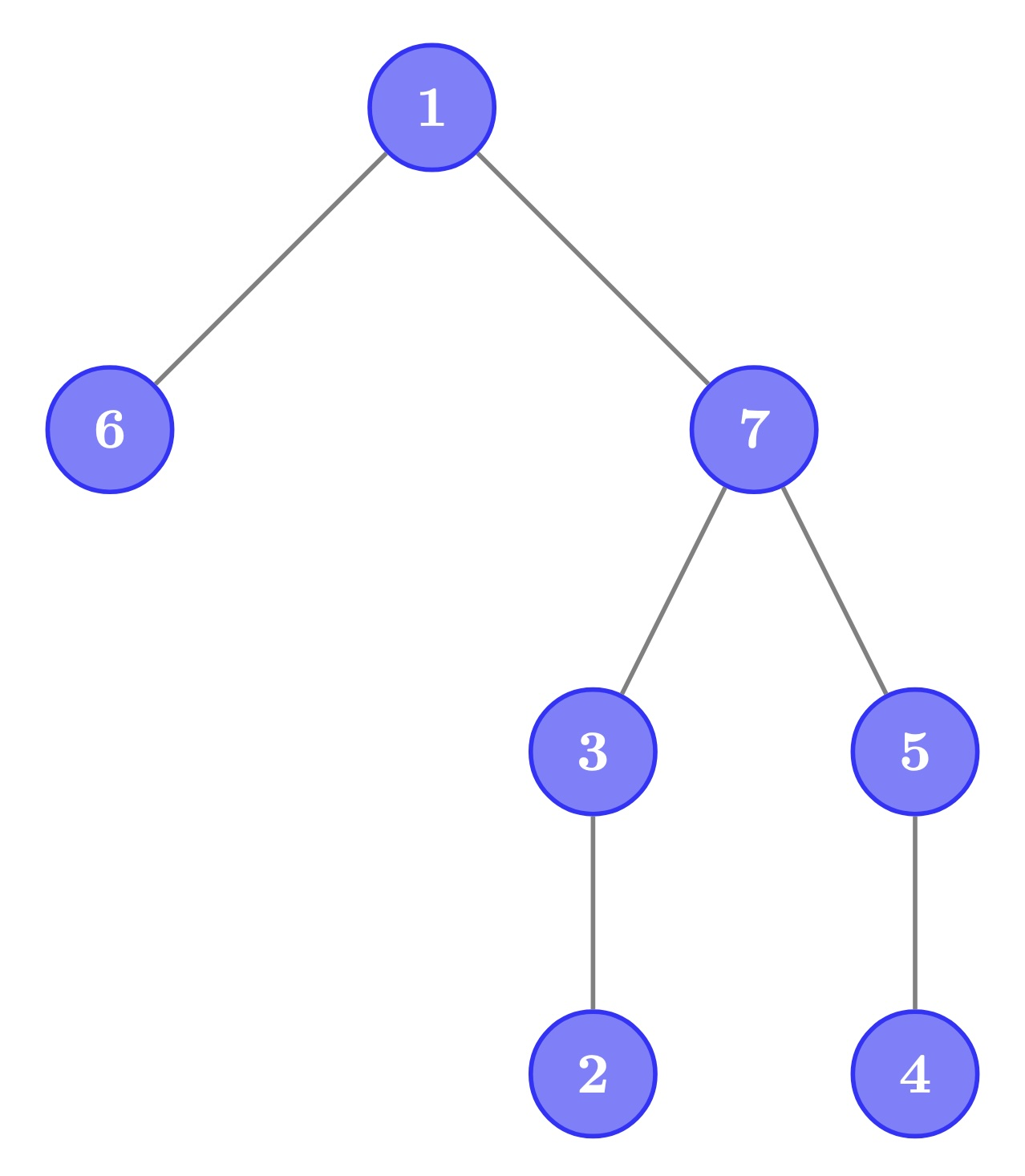 下图是该样例所对应的树结构：  测试用例 2： 初始状态：怪物在顶点 $\{2\}$。仅需一条路径 $1 \to 2$。答案为 $1$。 第一次查询后（$v=2$）：没有怪物。需要 $0$ 条路径。答案为 $0$。 第二次查询后（$v=1$）：怪物在顶点 $\{1,2\}$。仅需一条路径 $1 \to 2$。答案为 $1$。 由 ChatGPT 5 翻译