CF2155E Mimo & Yuyu

Mimo 和 Yuyu 刚刚拼好了一幅精美的 Bellas Artes 1000 片拼图！现在他们在寻找其他的娱乐方式。 有一个 $n \times m$ 的网格，列从左到右编号为 $1, 2, \ldots, m$，行从上到下编号为 $1, 2, \ldots, n$。设 $(u, v)$（$1 \le u \le n, 1 \le v \le m$）表示第 $u$ 行第 $v$ 列的网格单元。每个单元格可以包含任意数量的代币，且这些代币之间没有区别。初始时，有 $k$ 个代币，第 $i$ 个代币位于 $(x_i, y_i)$。 现在 Mimo 和 Yuyu 轮流进行游戏。每回合，当前玩家选择一个当前在网格上的代币 $c$，以及一个长度为 $p$ 的由不同单元格组成的序列 $(a_1, b_1), (a_2, b_2), \ldots (a_p, b_p)$（$p \ge 2$），满足以下条件： - $c$ 位于 $(a_1, b_1)$； - 对于所有 $i$ （$1 \le i < p$），有 $|a_{i+1} - a_i|+|b_{i+1} - b_i| = 1$，即序列中的相邻单元格必须在网格中相邻； - $b_1 \ge b_2 \ge \ldots \ge b_p$，即所有位置的列号按非递增排序（不能离开第 1 列的方向）； - $b_p = 1$，即序列的最后一个位置必须在第 1 列； - $b_1 > b_2$，特别地，$b_2 = b_1-1$，也就是说 $(a_1, b_1)$ 必须是唯一一个位于第 $b_1$ 列的单元格。 然后，玩家将 $c$ 从网格上移除，并在 $(a_2, b_2), (a_3, b_3), \ldots, (a_p, b_p)$ 上各增加 1 个代币。该回合结束。 无法进行操作的玩家判负。Mimo 先手。假设双方都采取最优策略，判定谁会获胜。 例如，考虑如下情景：$n=6$，$m=4$，当前有 3 个代币分别在 $(2, 3)$、$(4, 2)$ 和 $(6, 4)$（如图 1 所示）。在这种情况下，一种合法操作可以是选择 $(6, 4)$ 的代币 $c$，以及长度 $p=10$ 的序列，其中 $a=[6,6,5,4,3,2,2,3,4,4]$，$b=[4,3,3,3,3,3,2,2,2,1]$。注意 $(a_i, b_i)$ 在网格内为有效单元格。 为了便于理解，图 2 中用虚线给出了上述 $ (a_1, b_1), (a_2, b_2), \ldots, (a_p, b_p)$ 的顺序路径。图 3、4 分别展示了执行该操作后的局面（有无序列高亮）。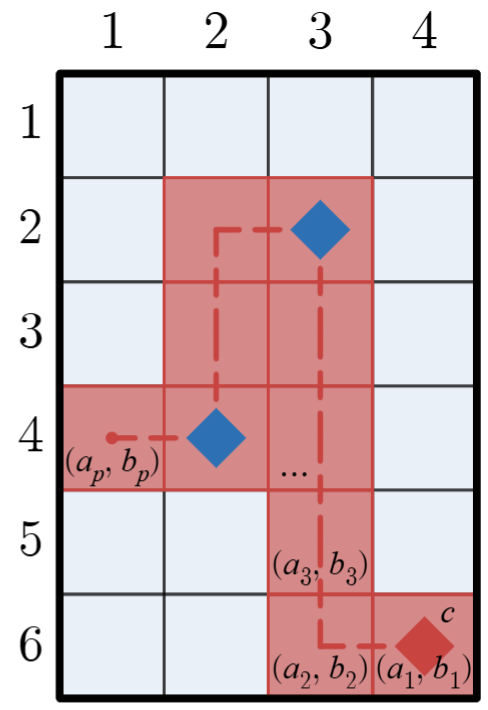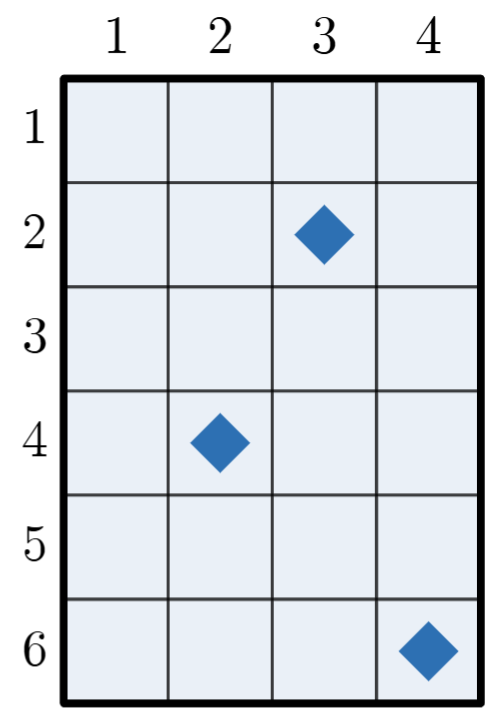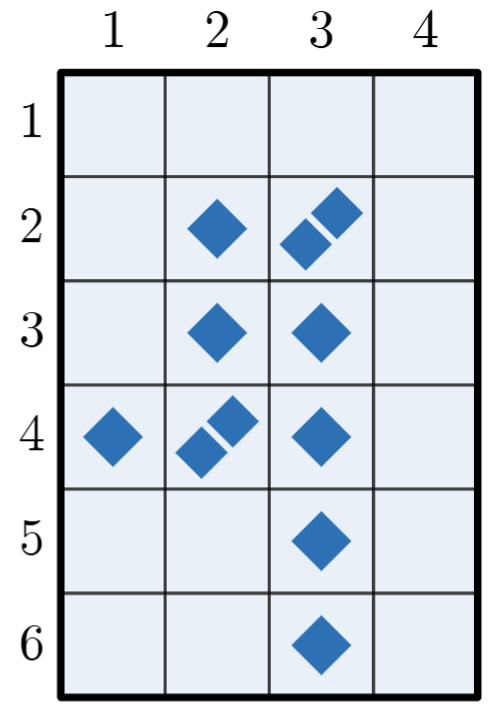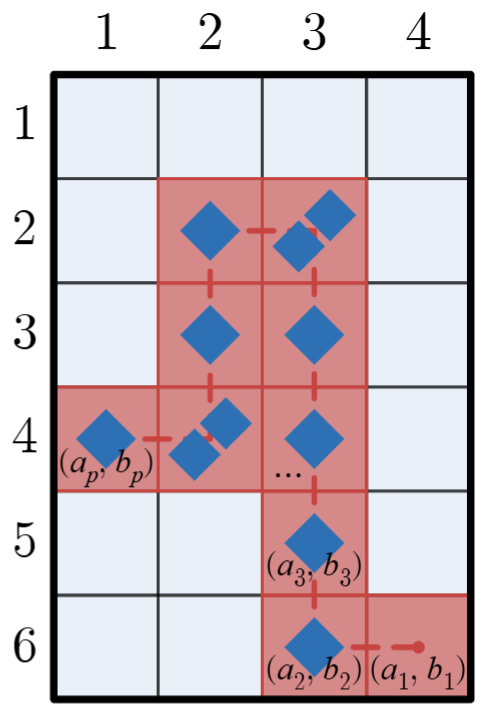 图 1 图 2 图 3 图 4 注意第一个和第七个样例与分别对应图 1 和图 4。

每组测试包含多组数据。第一行包含测试组数 $t$（$1 \le t \le 10^4$）。每组测试描述如下。 每组测试的第一行包含三个整数 $n$、$m$、$k$（$1 \le n, m, k \le 2 \cdot 10^5$）。 接下来的 $k$ 行，每行两个整数 $x_i$ 和 $y_i$（$1 \le x_i \le n, 1 \le y_i \le m$）。 保证所有测试组的 $k$ 之和不超过 $2 \cdot 10^5$。 注意 $n$ 和 $m$ 没有显式的和的上限。

对于每组测试，如果 Mimo 获胜，输出 Mimo；如果 Yuyu 获胜，输出 Yuyu。 输出不区分大小写，例如 mIMo、mimo、Mimo、MIMO 都会被认可为先手获胜。

在第二组样例中，Mimo 无法进行任何操作，因此 Yuyu 获胜。 在第三组样例里，$(1,1)$ 上的代币无法被作为 $c$ 用于任何一步操作，因为不存在满足 $b_1 > b_2$ 的序列，因此游戏可能进展如下： - Mimo 移除 $(1,2)$ 上的代币，并在 $(1,1)$ 上添加一个代币。 - Yuyu 移除 $(2,2)$ 上的代币，并在 $(2,1)$ 上添加一个代币。 - Mimo 移除 $(3,2)$ 上的代币，并在 $(3,1)$ 上添加一个代币。 可以证明，Yuyu 无法做得更好，因此 Mimo 获胜。 由 ChatGPT 5 翻译