CF2159F Grand Finale: Snakes

This is an interactive problem. You are given an integer $ n $ and an $ n\times n $ grid of numbers $ G $ . The grid of numbers contains each number from $ 1 $ to $ n^2 $ exactly once. Let's define a snake of length $ l $ as a deque $ [(x_1,y_1), (x_2,y_2), \ldots, (x_l,y_l)] $ , where $ (x_1,y_1) $ is the head of the snake, and $ (x_l,y_l) $ is the tail. At second $ 1 $ , $ x_1=x_2=\ldots = x_l=1 $ and $ y_i=i $ for all $ 1 \leq i \leq l $ . In other words, the snake is entirely located in the first row, with the head at $ (1,1) $ and the rest of the snake to the right of the head. Each subsequent second, the snake moves down or right in the grid. Formally, the tail $ (x_l,y_l) $ is removed, and either $ (x_1+1,y_1) $ or $ (x_1,y_1+1) $ is added as the new head. The first move of the snake is always downwards. It can be shown that the snake will never intersect itself under these restrictions. The snake will move exactly $ 2n-2 $ times, never moving outside the grid. At second $ 2n-1 $ , the head reaches $ (n,n) $ , and the movement stops. It can be shown that the snake moves exactly $ n-1 $ times to the right and exactly $ n-1 $ times downwards. There are $ n $ hidden snakes, with the $ i $ -th snake having length $ i $ for $ 1 \leq i \leq n $ , each moving independently according to the rule above. You do not know how the snakes move. Define $ f(l,T) $ as the maximum number that the snake with length $ l $ covers at second $ T $ . 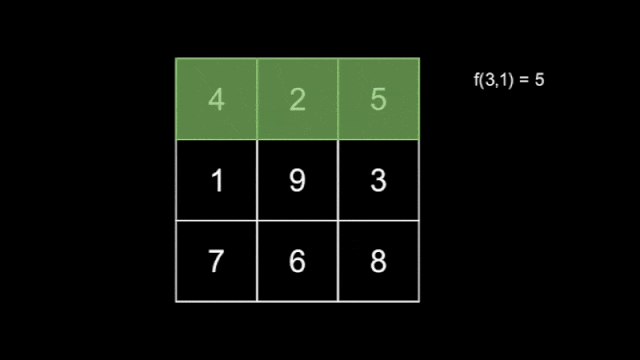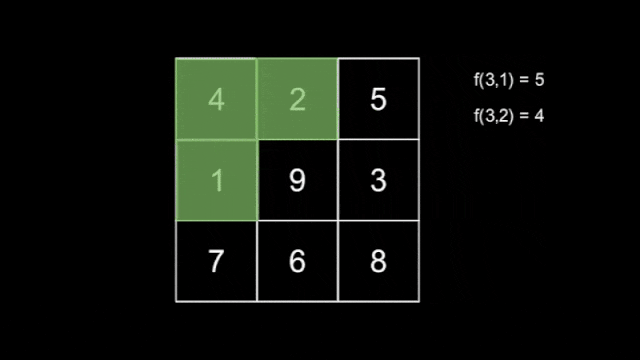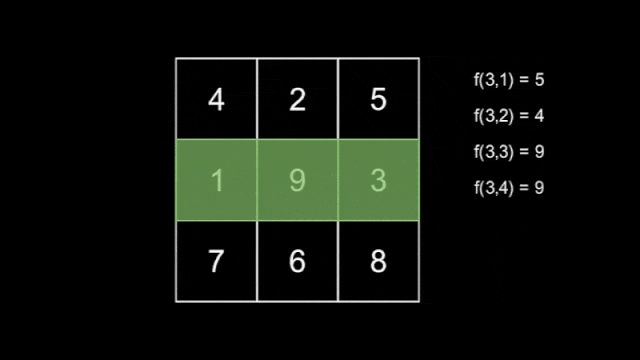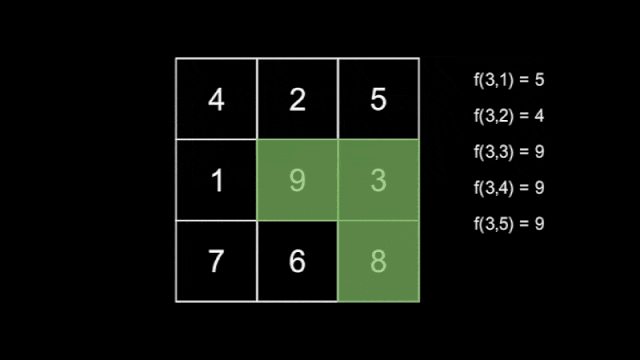 An example of a snake with length $ l=3 $ .Now, you are also given an integer $ m $ . Your task is to find the $ m $ smallest values of $ f(l,T) $ , using at most $ 120n+m $ queries asking for the value of $ f(l,T) $ for some $ 1 \leq l \leq n $ and $ 1 \leq T \leq 2n-1 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 2 \leq n \leq 500, 1 \leq m \leq n(2n-1) $ ). The following $ n $ lines contain the grid $ G $ . The $ i $ -th of these lines contains $ n $ integers $ G_{i,1}, G_{i,2}, \ldots, G_{i,n} $ ( $ 1 \leq G_{i,j} \leq n^2 $ ). It is guaranteed that $ G $ contains each number from $ 1 $ to $ n^2 $ exactly once. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 500 $ , and the sum of $ m $ over all test cases does not exceed $ 5\cdot 10^4 $ . After you read the $ n+1 $ lines of input, the interaction begins with your first query.

N/A

Below shows the tiles that the three snakes cover as they move across the grid. 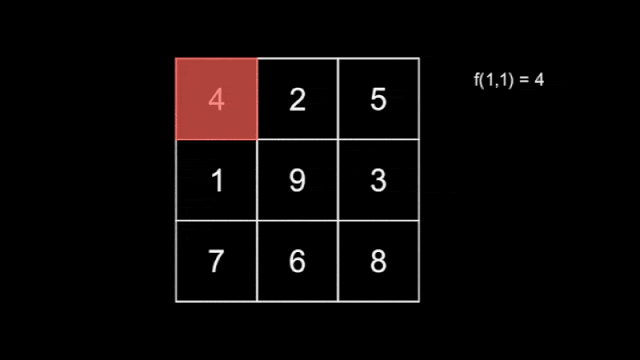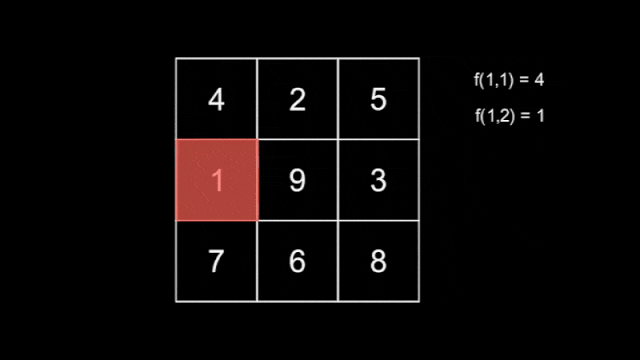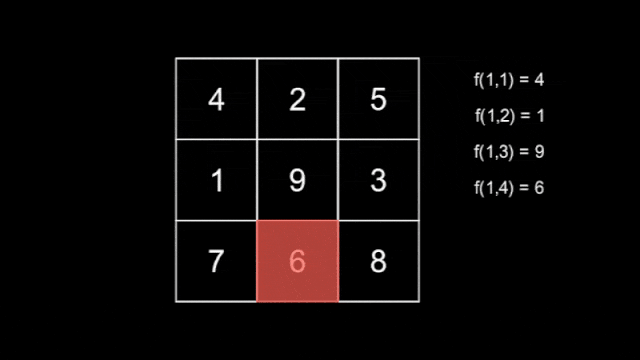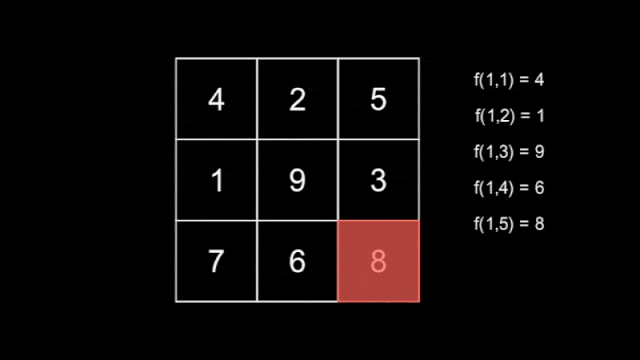 The tiles covered by the first snake. 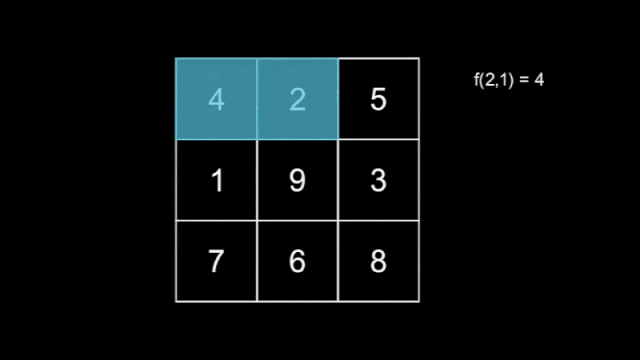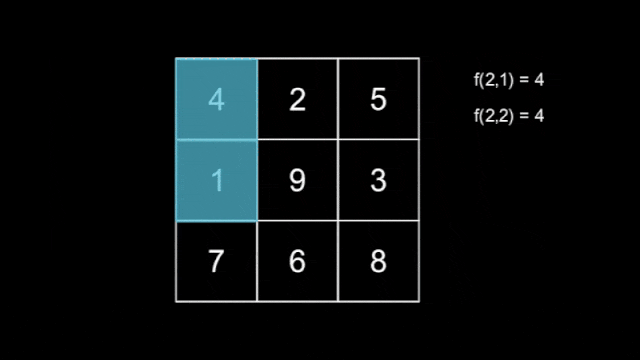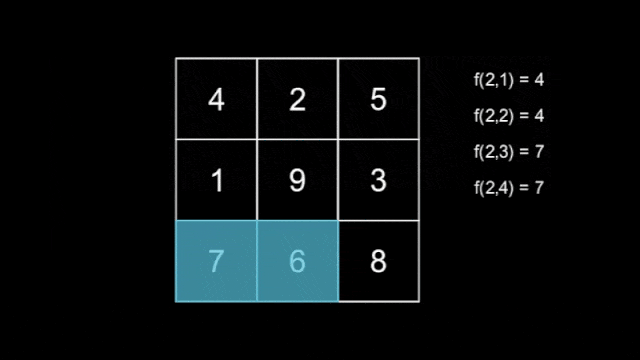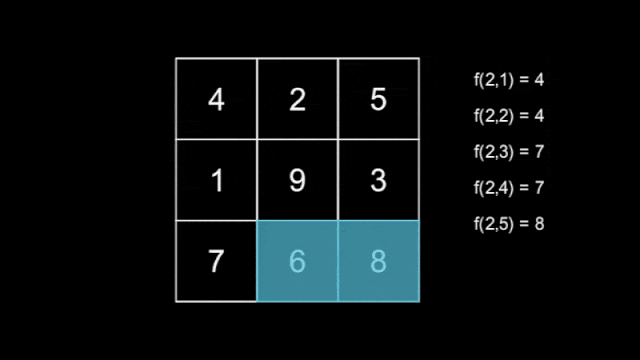 The tiles covered by the second snake.The tiles covered by the third snake are shown in the statement above.