CF215B Olympic Medal

世界编程奥林匹克奖牌是一枚金属圆盘，由两部分组成：第一部分是一个由金属制成的圆环，外半径为 $r_{1}$ 厘米，内半径为 $r_{2}$ 厘米 $(0 < r_{2} < r_{1})$，密度为 $p_{1}$ 克/立方厘米。第二部分是内半径为 $r_{2}$ 厘米的圆盘，由密度为 $p_{2}$ 克/立方厘米的金属制成。圆盘嵌套在圆环内部。 奥林匹克评审团决定 $r_{1}$ 可以取 $x_{1}, x_{2}, \ldots, x_{n}$ 这些可能的值之一，具体取哪一个由评审团决定。同样，$p_{1}$ 可以从 $y_{1}, y_{2}, \ldots, y_{m}$ 这些候选值中取一个，$p_{2}$ 可以从 $z_{1}, z_{2}, \ldots, z_{k}$ 这些候选值中选择一个。 根据最古老的传统，外环质量 $m_{out}$ 与内圆盘质量 $m_{in}$ 的比值应等于 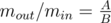，其中 $A,B$ 为古籍中记载的常数。现在，为了开始制作奖牌，评审团需要选择 $r_{1}$、$p_{1}$、$p_{2}$ 的具体数值，并计算出最合适的 $r_{2}$。 评审团希望选择能使半径 $r_{2}$ 最大的方案。请你帮助评审团找出这个最大的 $r_{2}$。$r_{2}$ 不必为整数。 奖牌的厚度在整个区域内都是均匀一致的，内圆盘的厚度与外环的厚度相同。

第一行输入一个整数 $n$ 和一列整数 $x_{1},x_{2},\ldots,x_{n}$。 第二行输入一个整数 $m$ 和一列整数 $y_{1},y_{2},\ldots,y_{m}$。 第三行输入一个整数 $k$ 和一列整数 $z_{1},z_{2},\ldots,z_{k}$。 最后一行输入两个整数 $A$ 和 $B$。 所有输入的数字均为正数，且不超过 $5000$。上述三组数各自内部的数字互不相同。每一行的数字用空格分隔。

输出一个实数，即最大化后的 $r_{2}$。允许的绝对或相对误差不超过 $10^{-6}$。保证本题存在满足要求的解。

在第一个样例中，评审团应选择如下数值：$r_{1}=3$，$p_{1}=2$，$p_{2}=1$。 由 ChatGPT 5 翻译