CF215C Crosses

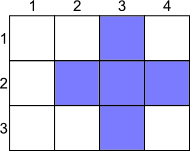
有一个大小为 $n$ 行 $m$ 列的棋盘，行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $m$。我们用 $(i,j)$ 表示位于第 $i$ 行第 $j$ 列的格子。 一个六元组 $(a,b,c,d,x_{0},y_{0})$（其中 $0 \leq a,b,c,d$）表示一个“十字”，并分配了一组格子。如果某个格子 $(x,y)$ 满足下列两个条件中的至少一个，就属于该集合： - $|x_{0}-x| \leq a$ 且 $|y_{0}-y| \leq b$ - $|x_{0}-x| \leq c$ 且 $|y_{0}-y| \leq d$  上图显示的是在 $3\times 4$ 的棋盘上，十字 $(0,1,1,0,2,3)$ 的样例。 你的任务是，找到有多少种不同的六元组 $(a,b,c,d,x_{0},y_{0})$，它们代表的十字面积等于 $s$，并且整个十字完全在 $n \times m$ 的棋盘内。若“十字”的任意一个格子没有越界（即对于每个属于该十字的 $(x, y)$，$1 \leq x \leq n$ 且 $1 \leq y \leq m$ 均成立），则认为该十字完全位于棋盘内。 这里“十字”的面积指的是它包含的格子的数量。 注意，如果表示它们的六元组不同（顺序亦不同），即使这两个十字所包含的格子集合完全重合，也认为它们是不同的。

输入包含一行，包含三个整数 $n$、$m$、$s$（$1 \leq n,m \leq 500$，$1 \leq s \leq n \cdot m$），整数之间用空格分隔。

输出一个整数，表示恰好有 $s$ 个格子的完全位于 $n \times m$ 棋盘上的不同“十字”六元组的数量。 请不要在 C++ 中使用 %lld 进行读写 64 位整数。推荐使用 cin/cout 或 %I64d。

第一个样例中，符合条件的六元组如下：$(0,0,0,0,1,1)$、$(0,0,0,0,1,2)$、$(0,0,0,0,2,1)$、$(0,0,0,0,2,2)$。 第二个样例中，符合条件的六元组如下：$(0,1,1,0,2,2)$、$(0,1,1,0,2,3)$、$(1,0,0,1,2,2)$、$(1,0,0,1,2,3)$。 由 ChatGPT 5 翻译