CF2161F SubMST

给定一棵无向无权树 $T$，包含 $n$ 个顶点。 定义一个完全无向加权图 $G$，有 $n$ 个顶点，其中 $G$ 中顶点 $u$ 和 $v$ 之间的边的权值等于原树中 $u$ 到 $v$ 的距离。 对于所有可能的顶点子集，考虑由这些顶点诱导出的 $G$ 的子图的最小生成树（MST）。计算所有可能顶点子集的 MST 权值之和。 由于答案可能很大，只需输出结果对 $10^9 + 7$ 取模后的值。

每个测试点包含多组测试数据。第一行包含测试用例个数 $t$（$1 \le t \le 10000$）。接下来是每组测试数据的描述。 每组测试数据第一行包含一个整数 $n$（$1 \leq n \leq 5000$），表示树的顶点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$），表示树中的一条边。 保证所有测试点中 $\sum n^2 \leq 5000^2$。

输出所有可能顶点子集的 MST 权值之和，结果对 $10^9+7$ 取模。

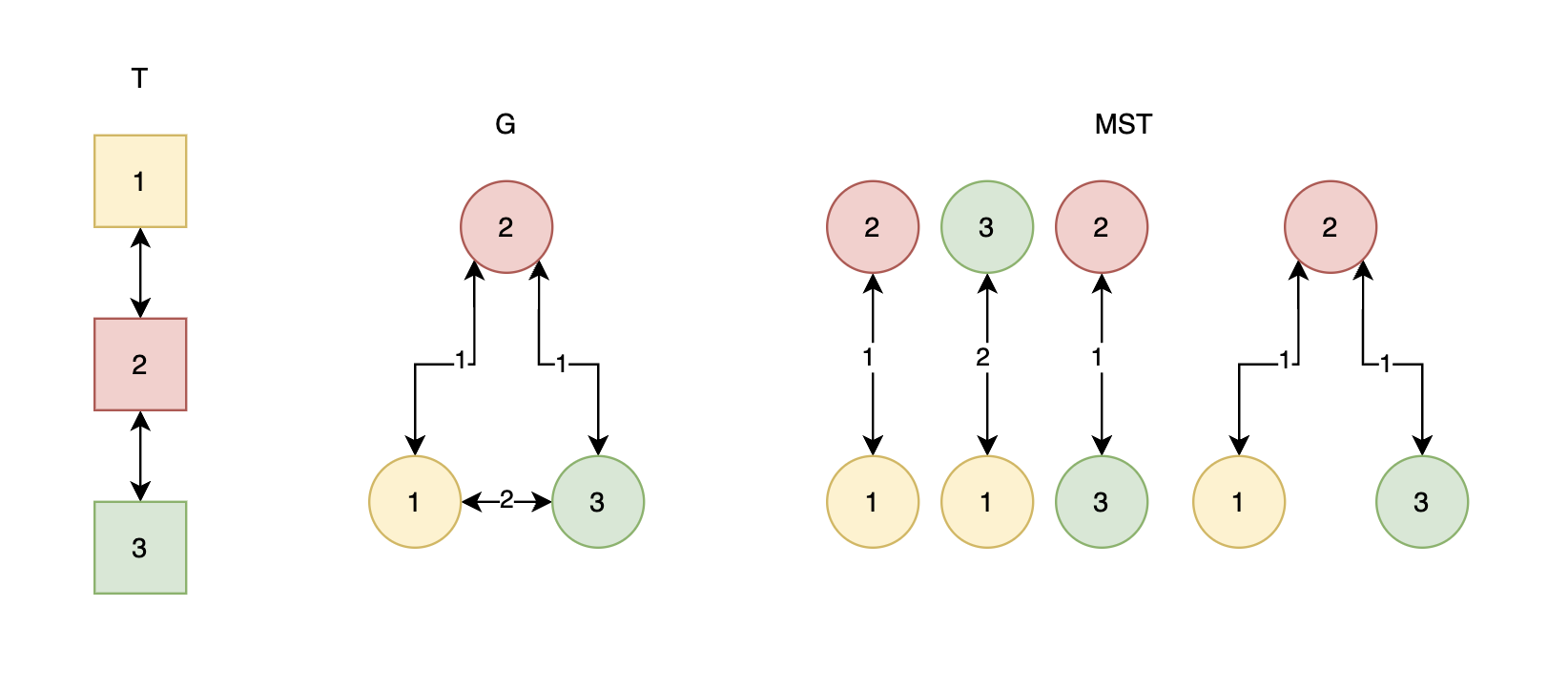
第一个测试用例如图所示。仅包含至多一个顶点的子集未予展示，因为这些子集的权值为 $0$，对答案没有贡献。  由 ChatGPT 5 翻译