CF2162G Beautiful Tree

A tree is a connected graph without cycles. A tree is called beautiful if the sum of the products of the vertex labels for all its edges is a perfect square. More formally, let $ E $ be the set of edges in the tree. The tree is called beautiful if the value $$$ S = \sum_{\{u, v\} \in E} (u \cdot v) $$$ is a perfect square. That is, there exists an integer $ x $ such that $ S = x^2 $ . You are given an integer $ n $ . Your task is to construct a beautiful tree having $ n $ vertices or report that such a tree does not exist.

The first line of input contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of testcases. Each testcase contains a single integer $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ). It is guaranteed that the sum of $ n $ over all the testcases does not exceed $ 2\cdot10^5 $ .

For each testcase, if there is no beautiful tree having $ n $ vertices, print $ -1 $ . Otherwise, print $ n-1 $ lines denoting the edges of a beautiful tree having $ n $ vertices. Each line should contain two space-separated integers $ u,v $ ( $ 1 \le u,v \le n $ ) representing an edge. The vertices can be printed in any order within an edge, and the edges can be printed in any order.

Test case 1: No beautiful tree exists with $ 2 $ vertices. Hence, print $ -1 $ . Test case 2: 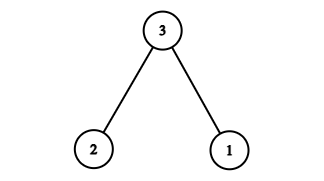 $ S = (2\cdot3) + (1\cdot3) = 9 = (3)^2 $ Test case 3: 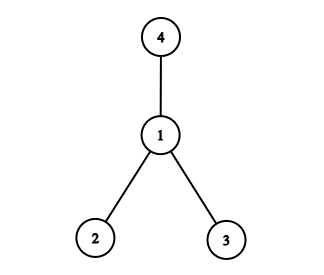 $ S = (2\cdot1) + (3\cdot1) + (4\cdot1) = 9 = (3)^2 $