CF2162G Beautiful Tree

树是一种没有环的连通图。 如果一棵树所有边的端点标签的乘积之和为完全平方数，则称这棵树是美丽的。 更正式地，设 $E$ 是树的边集。如果有 $$S = \sum_{\{u, v\} \in E} (u \cdot v)$$ 是一个完全平方数，即存在整数 $x$ 使得 $S = x^2$，则称这棵树是美丽的。 给定一个整数 $n$，你的任务是构造一个包含 $n$ 个顶点的美丽树，或者报告不存在这样的树。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的个数。 每个测试用例包含一个整数 $n$（$2 \le n \le 2\times10^5$）。 保证所有测试用例中 $n$ 的总和不超过 $2\times10^5$。

对于每个测试用例，如果不存在包含 $n$ 个顶点的美丽树，输出 $-1$。 否则，输出 $n-1$ 行，每行两个空格分隔的整数 $u, v$（$1 \le u, v \le n$），表示一条边。 同一条边的两个端点顺序可以互换，边的输出顺序不限。

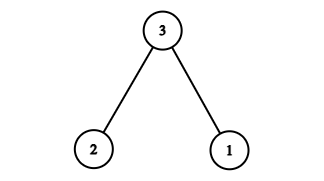
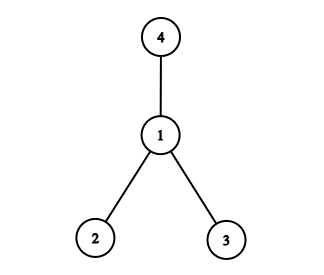
测试点 1：不存在包含 $2$ 个顶点的美丽树，因此输出 $-1$。 测试点 2：  $S = (2\cdot3) + (1\cdot3) = 9 = (3)^2$ 测试点 3：  $S = (2\cdot1) + (3\cdot1) + (4\cdot1) = 9 = (3)^2$ 由 ChatGPT 5 翻译