CF2165E Rainbow Branch

Given a tree with $ n $ vertices, you need to assign a color to each edge. Define the inconvenience of an assignment as the maximum number of colors on the path between any two vertices. You need to assign exactly $ k $ different colors (each color must appear at least once) to the edges while minimizing the inconvenience of the assignment. Please calculate the minimum inconvenience for all $ k=1,2,\ldots,n-1 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of the input contains one positive integer $ n $ ( $ 3\le n\le3\cdot10^5 $ ) — the number of vertices. The next $ n-1 $ lines each contain two positive integers $ u_i,v_i $ ( $ 1\le u_i,v_i\le n $ ) — indicating that there is an edge between vertices $ u_i $ and $ v_i $ . It is guaranteed that the edges in the input form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 3\cdot10^5 $ .

For each test case, print a single line containing $ n-1 $ integers. The $ i $ -th integer represents the minimum inconvenience for $ k=i $ .

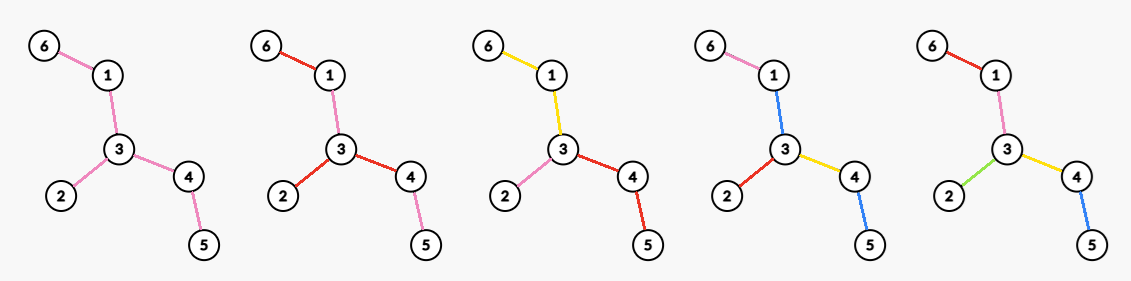
In the first test case, possible solutions for $ k=1,2,\ldots,n-1 $ are as follows: