CF2169D1 Removal of a Sequence (Easy Version)

This is the easy version of the problem. The difference between the versions is the constraint on $ x $ ; in this version, $ x \le 10^5 $ . Polycarp has a sequence of all natural numbers from $ 1 $ to $ 10^{12} $ . He decides to modify this sequence by performing the following action $ x $ times: - Simultaneously remove all numbers at positions $ y $ , $ 2 \cdot y $ , $ 3 \cdot y $ , ..., $ m \cdot y \le n $ , where $ n $ is the length of the current sequence. After that, Polycarp wants to find the $ k $ -th number in the remaining sequence or determine that the length of the resulting sequence is less than $ k $ . Help Polycarp solve this problem! Consider an example. 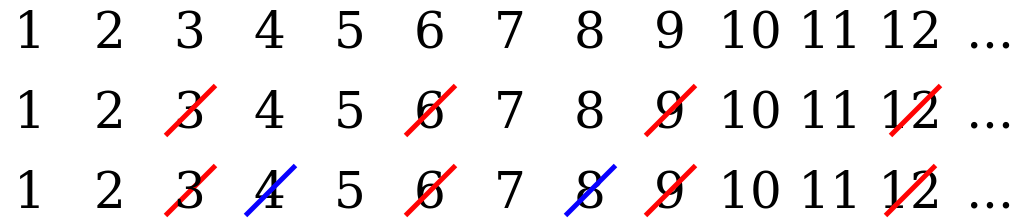Let $ x = 2 $ , $ y = 3 $ , $ k = 5 $ , then: The numbers crossed out with a red line were removed after the first operation, and the numbers crossed out with a blue line were removed after the second operation. Thus, the number at position $ k = 5 $ is the number $ 10 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10 $ ). The description of the test cases follows. The only line of each test case contains three integers $ x $ , $ y $ , $ k $ ( $ 1 \le x \le \bf{10^{5}} $ , $ 1 \le y, k \le 10^{12} $ ).

For each test case, output a positive integer that is at the $ k $ -th position in the resulting sequence, or $ -1 $ if the length of the resulting sequence is less than $ k $ .