CF2170A Maximum Neighborhood

考虑一个 $n \times n$ 的网格，填充规则如下： - 第一行从左到右填入 $1$ 到 $n$ 的整数； - 第二行从左到右填入 $(n+1)$ 到 $2n$ 的整数； - 以此类推，第 $n$ 行从左到右填入 $(n^2-n+1)$ 到 $n^2$ 的整数。 我们定义一个格子的代价为其格子上的数值加上所有相邻格子的数值之和。若两个格子共享一条边，则被视为相邻。 你的任务是计算网格中所有格子代价的最大值。 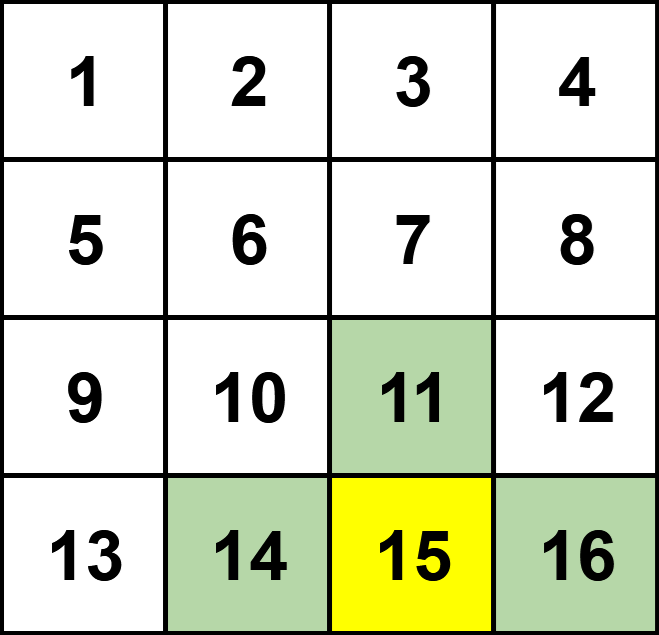 上图为 $n=4$ 的网格以及对应的最优解。其中黄色格子的代价最大，绿色格子为其相邻格子。该格子的代价为 $15 + 11 + 14 + 16 = 56$。

第一行包含一个整数 $t$（$1 \le t \le 100$）——表示测试用例数量。 接下来每个测试用例包含一行，一个整数 $n$（$1 \le n \le 100$）。

对于每个测试用例，输出一个整数——该网格中所有格子的最大代价。

在第一个例子中，只有 $1$ 个格子，代价为 $1$。 在第二个例子中，值为 $4$ 的格子代价最大：$4 + 2 + 3 = 9$。 在第三个例子中，值为 $8$ 的格子代价最大：$8 + 5 + 7 + 9 = 29$。 在第四个例子中，值为 $15$ 的格子代价最大：$15 + 11 + 14 + 16 = 56$。 在第五个例子中，值为 $19$ 的格子代价最大：$19 + 14 + 18 + 20 + 24 = 95$。 由 ChatGPT 5 翻译