CF2170A Maximum Neighborhood

Consider an $ n \times n $ grid filled with numbers as follows: - the first row contains integers from $ 1 $ to $ n $ from left to right; - the second row contains integers from $ (n+1) $ to $ 2n $ from left to right; - this pattern continues until the $ n $ -th row, which contains integers from $ (n^2-n+1) $ to $ n^2 $ from left to right. Let's define the cost of a cell as its value plus the sum of its neighboring cells' values. Two cells are considered neighboring if they share a side. Your task is to calculate the maximum cost among all cells in the grid. 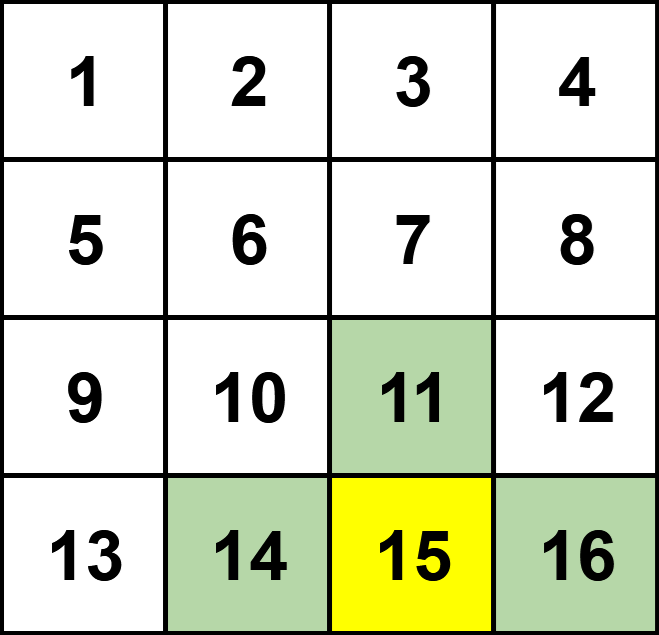 The grid for $ n = 4 $ and the optimal answer for it. The yellow cell has the maximum possible cost; the green cells are its neighbors. The cost of the cell is $ 15+11+14+16=56 $ .

The first line contains a single integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases. The only line of each test case contains a single integer $ n $ ( $ 1 \le n \le 100 $ ).

For each test case, print a single integer — the maximum cost among all cells in the grid.

In the first example, there is only $ 1 $ cell with the cost $ 1 $ . In the second example, the cell with value $ 4 $ has the maximum cost: $ 4 + 2 + 3 = 9 $ . In the third example, the cell with value $ 8 $ has the maximum cost: $ 8 + 5 + 7 + 9 = 29 $ . In the fourth example, the cell with value $ 15 $ has the maximum cost: $ 15 + 11 + 14 + 16 = 56 $ . In the fifth example, the cell with value $ 19 $ has the maximum cost: $ 19 + 14 + 18 + 20 + 24 = 95 $ .