CF2172B Buses

There is a long straight road of length $ \ell $ meters, where position $ p $ denotes the point on the road that is $ p $ meters away from the starting point. Along this road, there are $ n $ buses moving in the positive direction, each traveling at the same constant speed of $ x $ meters per minute. The $ i $ -th bus is currently at position $ s_i $ and continues moving until it reaches its designated destination at position $ t_i $ . Once a bus reaches its destination, it ceases operation and all passengers must disembark. There are also $ m $ people who wish to reach the end of the road (position $ \ell $ ). The current position of the $ i $ -th person is $ p_i $ , and each person can walk at a speed of at most $ y $ meters per minute. If a person is at the same position as a bus, they may hop on the bus instantly. While riding a bus, they may hop off at any moment. The time required to board or leave a bus is considered negligible. Buses always move at a constant speed $ x $ and never wait for passengers. Your task is to determine the minimum possible time for each person to reach the end of the road. 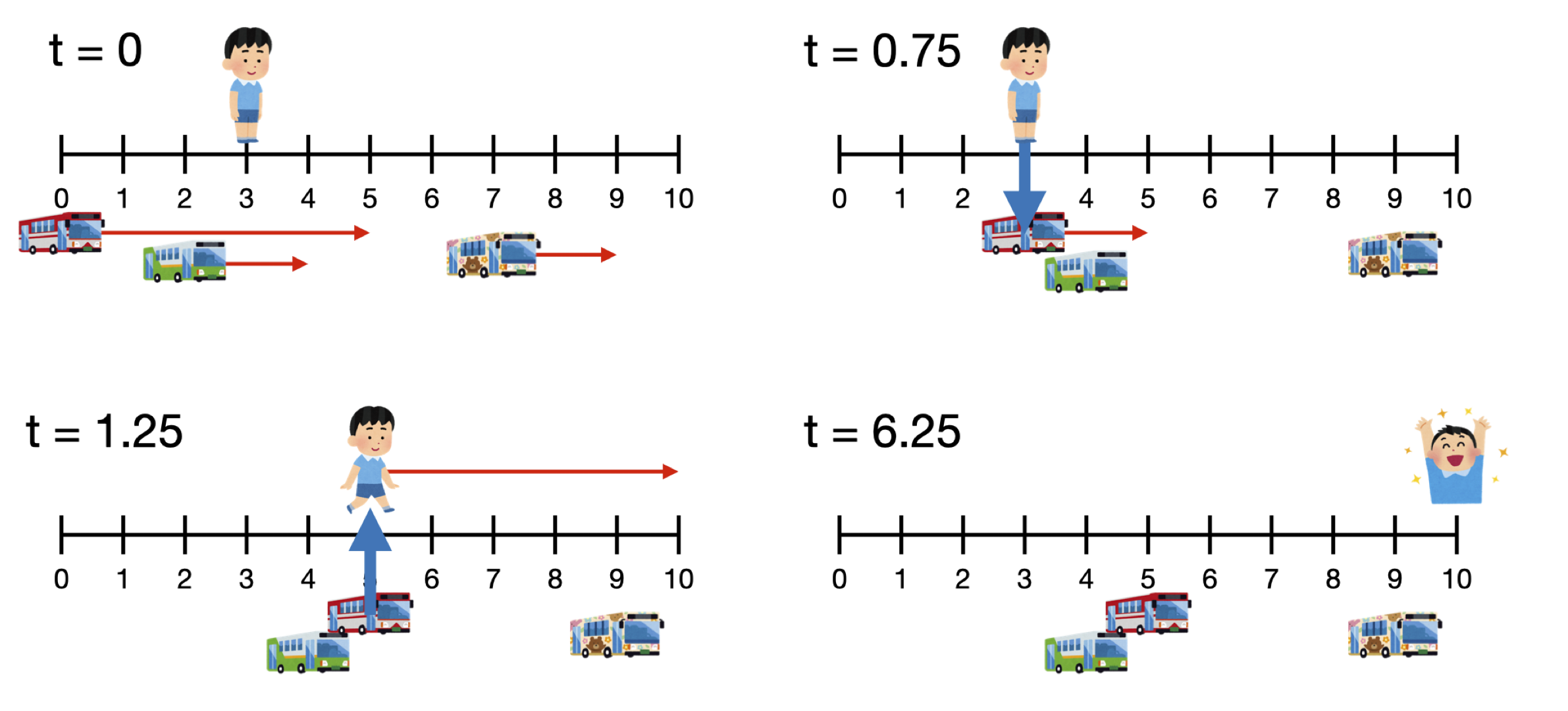 Figure 1: An illustration for sample input 1.

The first line contains five integers $ n $ , $ m $ , $ \ell $ , $ x $ and $ y $ , representing the number of buses, the number of people, the length of the road, the speed of the buses, and the walking speed of the people, respectively. The $ i $ -th of the following $ n $ lines contains two integers $ s_i $ and $ t_i $ , representing the starting position and the destination position of the $ i $ -th bus. The $ i $ -th of the following $ m $ lines contains one integer $ p_i $ , representing the current position of the $ i $ -th person. - $ 1 \leq n \leq 2 \times 10^5 $ - $ 1 \leq m \leq 2 \times 10^5 $ - $ 1 \leq \ell \leq 10^9 $ - $ 1 \leq y < x \leq 10^6 $ - $ 0 \leq s_i < t_i \leq \ell $ - $ 0 \leq p_i \leq \ell $

Print $ m $ lines. The $ i $ -th line contains a number which is the minimum time (in minutes) for the $ i $ -th person to reach the end of the road. Your answer will be accepted if the absolute or relative error does not exceed $ 10^{-6} $ . Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer is considered correct if $ \frac{\left\vert a - b \right\vert}{\max(1, \left\vert b \right\vert)} \leq 10^{-6} $ .

Explanation of Sample 1: A person initially at position $ p = 3 $ can reach the end of the road in $ 6.25 $ minutes as follows: - Wait for Bus 1 to arrive. - Hop on the bus and ride it until it reaches its destination at position $ t_1 = 5 $ . - Get off the bus and walk the remaining distance to position $ \ell = 10 $ . As shown in Figure 1, the total time spent is $ 6.25 $ minutes, which is the minimum possible.