CF2172C Circles Are Far from Each Other

给定 $n$ 个圆，以及两个整数参数 $k$ 和 $\ell$。第 $i$ 个圆的半径为 $r_i$，并且对所有 $1 \le i < j \le n$ 有 $r_i \ge r_j$。你的任务是在二维平面内绘制这 $n$ 个圆，使得同时满足以下条件。在描述条件之前，我们先回顾相关定义： - 每个圆由其圆心 $O$ 和半径 $r$ 唯一确定。 - 半径为 $r$ 的圆定义为所有与圆心 $O$ 的距离恰为 $r$ 的点的集合。本题所有距离均为欧几里得距离。 - 圆的内部区域定义为距离圆心 $O$ 小于 $r$ 的所有点的集合。 - 若圆 $C$ 能将另一个圆 $C^\prime$ 完全包含在其内部区域，则称 $C$ 包含 $C^\prime$。 请布局这 $n$ 个圆，使得下列所有条件同时满足： 1. 所有圆的圆心共线。 2. 任意两个圆心之间的距离不超过 $k$。 3. 任意两个圆不相交。 4. 若某个圆 $C$ 包含了两个圆 $C$ 和 $C^\prime$，则 $C$ 和 $C^\prime$ 必定存在包含关系（二者之一包含另一个）。 5. 第 $1$ 到第 $\ell$ 个圆可以被其它圆包含，也可以不被包含；其余 $n-\ell$ 个圆必须被至少一个圆包含。 一个满足上述所有条件的布局称为可行布局。对于一个可行布局 $\mathcal{A}$，定义其质量 $d(\mathcal{A})$ 为任意两个属于不同圆的点之间的最小距离。 如果存在至少一个可行布局，请输出所有可行布局中最大的质量。如果不存在可行布局，请输出 $0$。 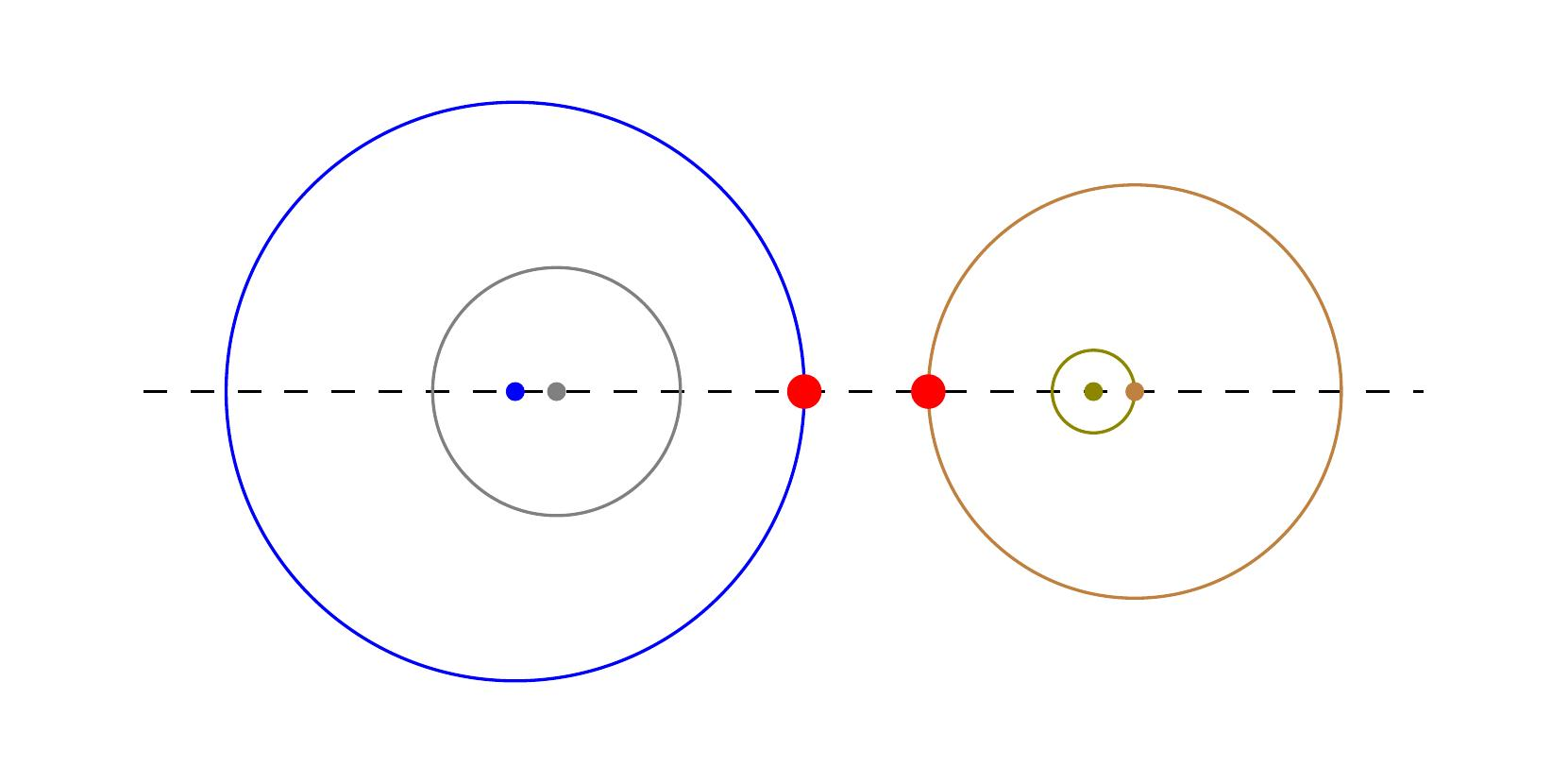 样例输入 1 的一种可行布局。 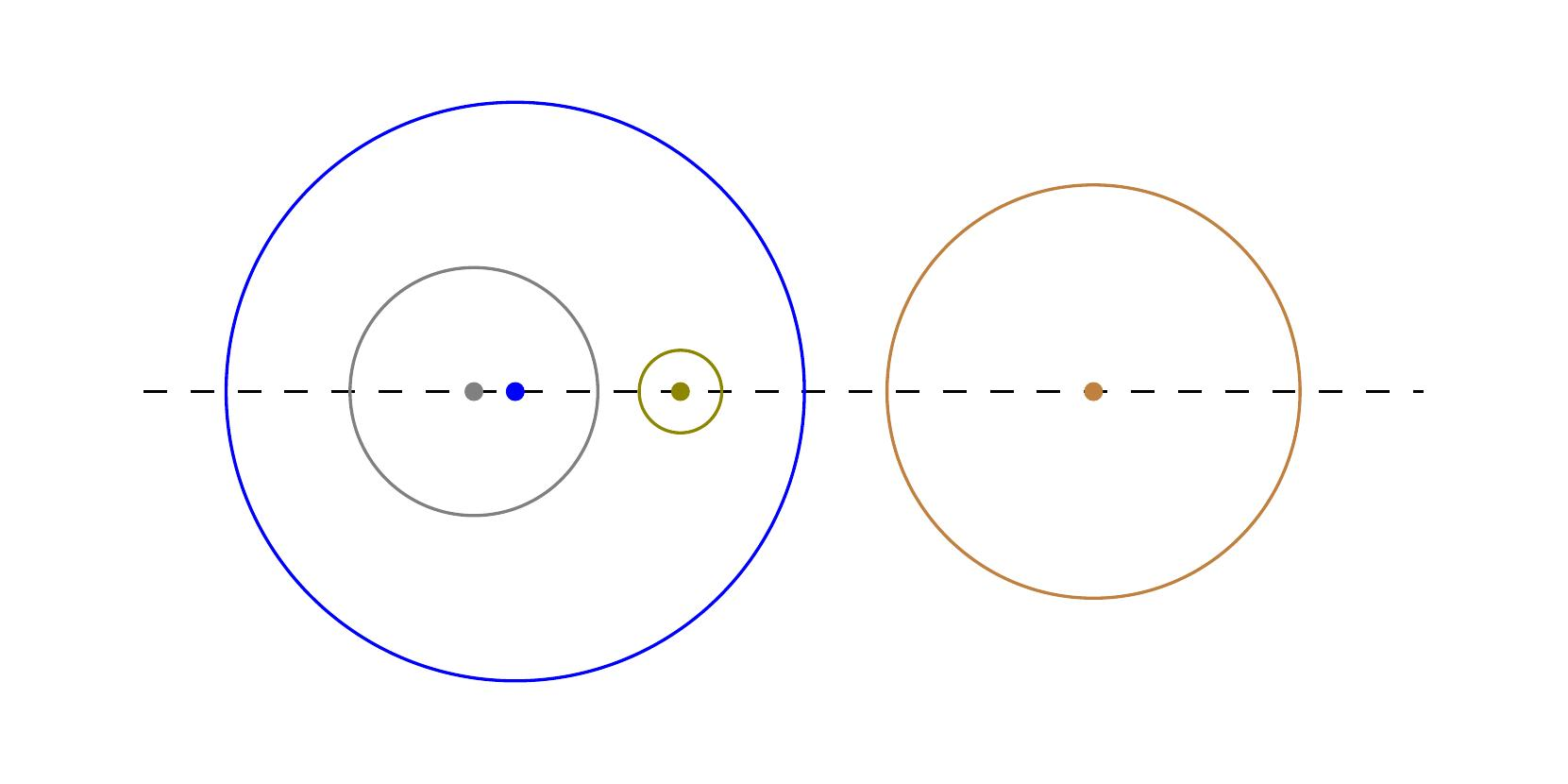 样例输入 1 的一种不可行布局。

第一行包含三个整数 $k$、$n$ 和 $\ell$，分别表示圆心之间最大距离、要绘制的圆的个数，以及可以不被其它圆包含的圆的数量。 第二行包含 $n$ 个整数 $r_1, r_2, \ldots, r_n$，其中 $r_i$ 表示第 $i$ 个圆的半径。 - $1 \le k \le 10^9$ - $2 \le n \le 10^5$ - $1 \le \ell \le \min\{n, 200\}$ - $1 \le r_i \le 10^9$ - 对所有 $1 \le i < j \le n$ 有 $r_i \ge r_j$

如果不存在可行布局，输出一个整数 $0$。 否则，输出所有可行布局 $\mathcal{A}$ 中最大的质量 $d(\mathcal{A})$，其输出格式如下： - 若 $d(\mathcal{A})$ 是整数，直接输出该整数。 - 若 $d(\mathcal{A})$ 不是整数，以最简分数 $a/b$ 的形式输出，其中 $1 \le a, b \le 10^9$，$\gcd(a,b)=1$，且 $|d(\mathcal{A})-a/b|$ 最小。如果有多种满足条件的写法，输出任意一种。

样例 1 说明：如图 1 所示为一种可行布局，每个圆及其圆心用不同的颜色表示。 在该布局中，不同圆的任意两点之间的最小距离为 $3$，用红点标记了这两个点。因此该布局的质量为 $3$，这是本例所有可行布局中可能的最大值。仅圆 $4$ 必须被另一圆包含，其余圆可以被包含也可以不被包含。 图 2 为不可行布局。在该布局中，圆 $1$ 同时包含了圆 $3$ 和圆 $4$，但 $3$ 和 $4$ 之间互不包含，违反了条件 4。 由 ChatGPT 5 翻译