CF2172K Kindergarten Homework

Kenny 是一名幼儿园老师，他正在教学生们数学。为了帮助他们学习，他希望以一种有趣且不令人厌烦的方式布置作业——数字搜寻游戏。 数字搜寻谜题类似于单词搜索谜题，但它不是寻找单词，而是寻找数学表达式。每个谜题由两部分组成：一个有 $n$ 行 $m$ 列的网格，以及一个目标数字列表 $a_1, a_2, \dots, a_q$。网格中的每个格子包含 1 到 9 的数字、加号 + 或乘号 *。 你可以通过连接同一行、同一列或同一对角线（任意方向）上的一个或多个连续字符，按直线（正反两个方向均可）形成一个表达式。每个表达式由其起始格和结束格唯一确定。如果两个表达式的起点或终点不同，即使内容完全相同，也视为不同的表达式。 一个合法表达式必须是如下形式： $$ num \quad op \quad num \quad op \ \dots \ op \quad num $$ 其中每个 $num$ 是由一个或多个数字组成的数字串，每个 $op$ 是 + 或 *。例如，“123”和“1+2*3+45”是合法表达式，“+123”和“2**5”不是。表达式的值按通常的算术规则计算（即乘法优先级高于加法）。 你的目标是，对于每个目标数字 $a_i$，计算网格中有多少个不同的合法表达式，其计算结果为 $a_i$。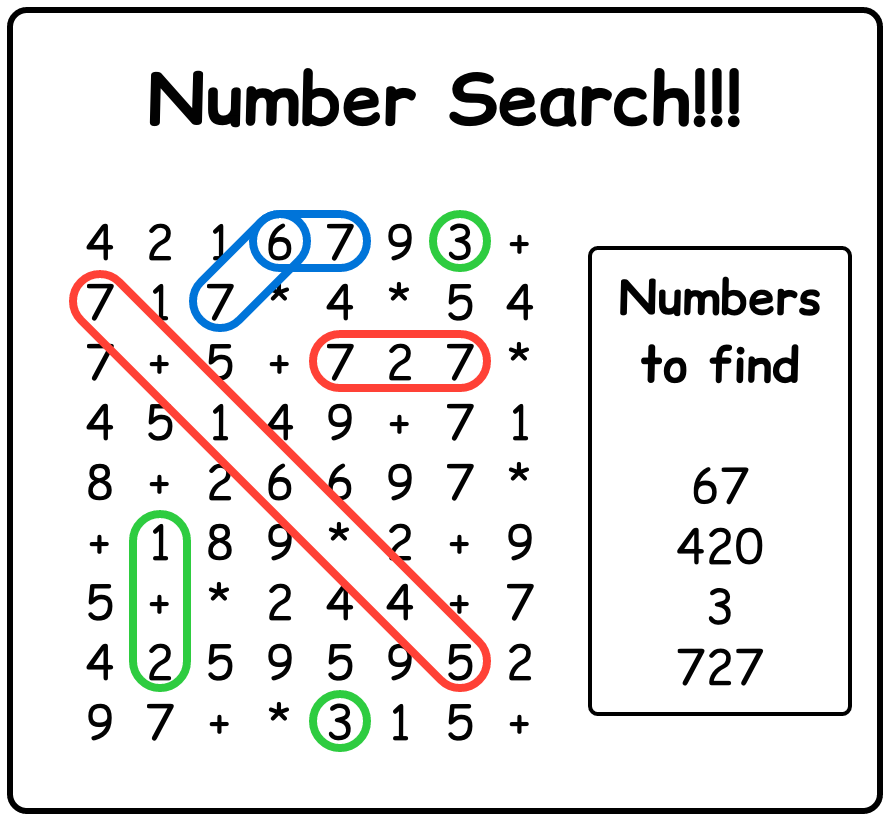 下面以一个完成的数字搜寻谜题为例：  记第 $r$ 行第 $c$ 列的格子为 $(r, c)$。 1. $67$ 的答案是 $2$，即在 $(1, 4)$ 开始的两个“67”表达式。虽然内容相同，但由于终点位置不同，视为两个不同表达式。 2. $420$ 的答案是 $0$，即没有任何表达式计算结果为 $420$。 3. $3$ 的答案是 $4$： - 表达式“3”出现在 $(1,7)$ 和 $(9,5)$。 - 表达式“1+2”出现在 $(6,2)$ 到 $(8,2)$。 - 表达式“2+1”出现在 $(8,2)$ 到 $(6,2)$。即使它们经过同一组格子，由于起点不同，也视为不同。 4. $727$ 的答案是 $3$： - 表达式“7+16*45”出现在 $(2,1)$ 到 $(8,7)$。注意先算乘法再算加法。 - 表达式“727”出现在 $(3,5)$ 到 $(3,7)$，以及 $(3,7)$ 到 $(3,5)$。它们内容相同，但视为两个不同表达式，因为起点不同。 Kenny 迫不及待希望看到孩子们享受这些有趣的数字搜寻谜题。但是，在给孩子们出题前，他需要先知道谜题的答案。请你帮助他计算每个谜题的答案。

第一行包含三个整数 $n$、$m$ 和 $q$，分别表示网格的行数、列数和目标数字的个数。 接下来 $n$ 行，每行包含一个长度为 $m$ 的字符串，表示网格内容。 接下来的 $q$ 行，每行包含一个整数 $a_i$，表示第 $i$ 个目标数字。 - $1 \leq n, m \leq 1000$ - $1 \leq n \times m \leq 3 \times 10^4$ - $1 \leq q \leq 10^5$ - 网格只包含字符 “123456789+*”。 - $1 \leq a_i \leq 10^6$ - 所有 $a_i$ 互不相同。

输出 $q$ 行，每行一个整数，第 $i$ 行表示目标数字 $a_i$ 的答案。

由 ChatGPT 5 翻译