CF2172M Maximum Distance To Port

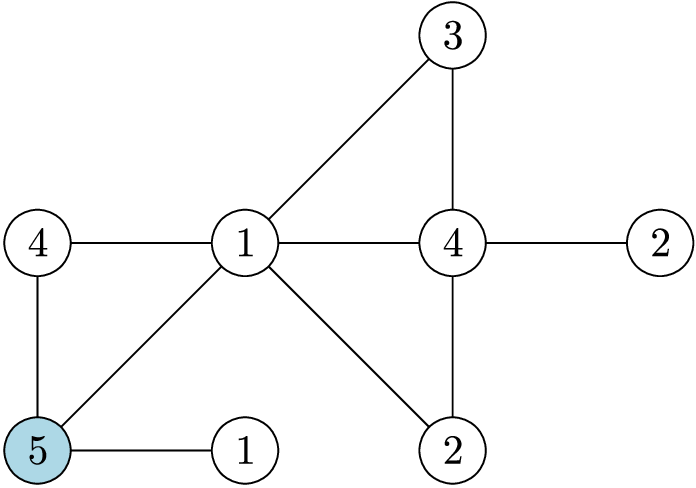
有 $n$ 个城市，编号从 $1$ 到 $n$，通过 $m$ 条双向道路相连，每条道路长度恰好为 $1$ 千米。整个道路网络构成一个连通的简单图。 每个城市恰好生产一种编号为 $1$ 到 $k$ 的农产品。城市 $1$ 是主要港口，所有产品都必须运送到这里。 政府希望估算出口农产品的最坏情况下的运输成本和时间。为此，他们需要计算对于每种产品类型，从生产该产品的任意城市到港口城市的最短距离中的最大值（单位为千米）。 你的任务是，对于每种产品类型，计算这个最大最短距离。  图 1：示例输入 2 的示意图。

第一行包含三个整数 $n$、$m$、$k$，分别表示城市数量、双向道路数量、产品种类数量。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$，其中 $a_i$ 表示城市 $i$ 生产的产品类型。 接下来的 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$，表示第 $i$ 条双向道路连接城市 $u_i$ 和 $v_i$。 - $1 \leq n \leq 2 \times 10^{5}$ - $0 \leq m \leq 2 \times 10^{5}$ - $1 \leq k \leq n$ - $1 \leq a_i \leq k$ - $1 \leq u_i, v_i \leq n$ - 图是连通且简单的（无自环或重边）。 - 每种产品类型 $1$ 到 $k$ 均至少由一个城市生产。

输出 $k$ 个整数，空格分隔。第 $i$ 个整数表示生产第 $i$ 种产品的所有城市到港口城市 $1$ 的最短距离中的最大值（单位为千米）。

示例 2 说明：图 1 展示了该示例。港口为蓝色节点。所有 5 号产品都已在港口，因此其运输成本为 $0$。而 4 号产品的运输成本较高：其中一个生产城市距离港口 1 千米，另一个距离港口 2 千米，所以运输成本为 $2$。 由 ChatGPT 5 翻译