CF2176D Fibonacci Paths

You are given a directed graph consisting of $ n $ vertices and $ m $ edges. Each vertex $ v $ corresponds to a positive number $ a_v $ . Count the number of distinct simple paths $ ^{\text{∗}} $ consisting of at least two vertices, such that the sequence of numbers written at the vertices along the path forms a generalized Fibonacci sequence. In this problem, we will consider that the sequence of numbers $ x_0, x_1, \ldots, x_k $ forms a generalized Fibonacci sequence if: - $ x_0, x_1 $ are arbitrary natural numbers. - $ x_i = x_{i - 2} + x_{i - 1} $ for all $ 2 \le i \le k $ . Note that a generalized Fibonacci sequence consists of at least two numbers. Since the answer may be large, output it modulo $ 998\,244\,353 $ . $ ^{\text{∗}} $ A simple path in a directed graph is a sequence of vertices $ v_1, v_2, \ldots, v_k $ such that each vertex in the graph appears in the path at most once and there is a directed edge from $ v_i $ to $ v_{i+1} $ for all $ i < k $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains two numbers $ n $ , $ m $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 1 \le m \le 2 \cdot 10^5 $ ) — the number of vertices and the number of edges in the graph, respectively. The second line of each test case contains $ n $ natural numbers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 10^{18} $ ) — the numbers written at the vertices. The next $ m $ lines contain the edges of the graph; each edge is defined by two natural numbers $ v, u $ ( $ 1 \le v, u \le n $ , $ u \neq v $ ), denoting a directed edge from $ v $ to $ u $ . It is guaranteed that there are no multiple edges in the graph. It is guaranteed that the sum of $ n $ and the sum of $ m $ across all test cases do not exceed $ 2 \cdot 10^5 $ .

For each test case, output the number of paths that form a generalized Fibonacci sequence, modulo $ 998\,244\,353 $ .

Explanation of the first test case example (the vertex number is outside the brackets, the number written in the vertex is inside): 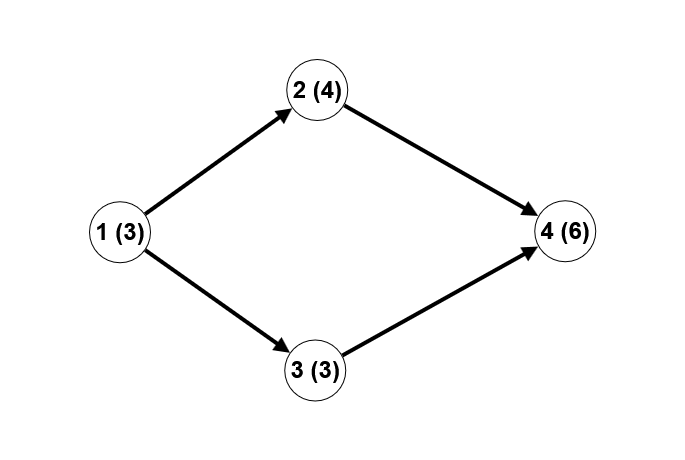 In this case, there are 5 generalized Fibonacci paths: ( $ 1, 2 $ ), ( $ 1, 3 $ ), ( $ 2, 4 $ ), ( $ 3, 4 $ ), ( $ 1,3,4 $ ). For example, for the path ( $ 1,3,4 $ ), the sequence of numbers written at the vertices along this path is: \[ $ 3,3,6 $ \]. As can be easily seen, the third number in the sequence is the sum of the two previous ones.Explanation of the second test case example: 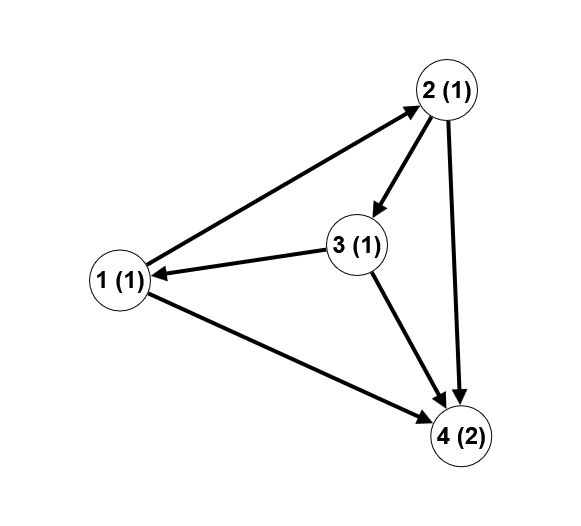 In this case, there are 9 generalized Fibonacci paths: ( $ 1, 2 $ ), ( $ 1, 4 $ ), ( $ 2, 3 $ ), ( $ 2, 4 $ ), ( $ 3, 1 $ ), ( $ 3, 4 $ ), ( $ 1, 2, 4 $ ), ( $ 2, 3, 4 $ ), ( $ 3, 1, 4 $ ). Note that for the path ( $ 1, 2, 3 $ ), the sequence of numbers written at the vertices along this path is: \[ $ 1,1,1 $ \], and it is not a generalized Fibonacci sequence.