CF2176D Fibonacci Paths

给定一个包含 $n$ 个顶点和 $m$ 条边的有向图。每个顶点 $v$ 上对应一个正整数 $a_v$。请你统计所有由至少两个顶点组成的不同简单路径，使得沿路径经过顶点的数字序列构成一个广义斐波那契数列。 在本题中，若数列 $x_0, x_1, \ldots, x_k$ 满足以下条件，则称其为广义斐波那契数列： - $x_0, x_1$ 为任意自然数。 - 对所有 $2 \le i \le k$，都有 $x_i = x_{i-2} + x_{i-1}$。 注意，广义斐波那契数列至少包含两个数字。 由于答案可能很大，输出其对 $998\,244\,353$ 取模的结果。 一个简单路径指在有向图中按顺序经过顶点 $v_1, v_2, \ldots, v_k$，且所有顶点至多出现一次，并且对于所有 $i < k$，存在从 $v_i$ 到 $v_{i+1}$ 的有向边。

每个测试点包含若干组测试数据。第一行为测试数据组数 $t$（$1 \le t \le 10^4$）。每组测试数据包括： 第一行，两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$1 \le m \le 2 \cdot 10^5$）——图中顶点数和边数。 第二行为 $n$ 个正整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 10^{18}$）——每个顶点上的数字。 接下来 $m$ 行，每行两个正整数 $v, u$（$1 \le v, u \le n$，$u \ne v$），表示一条从 $v$ 到 $u$ 的有向边。保证不存在重边。 保证所有测试数据中 $n$ 的总和与 $m$ 的总和不超过 $2 \times 10^5$。

对于每组测试数据，输出广义斐波那契路径的数量，对 $998\,244\,353$ 取模。

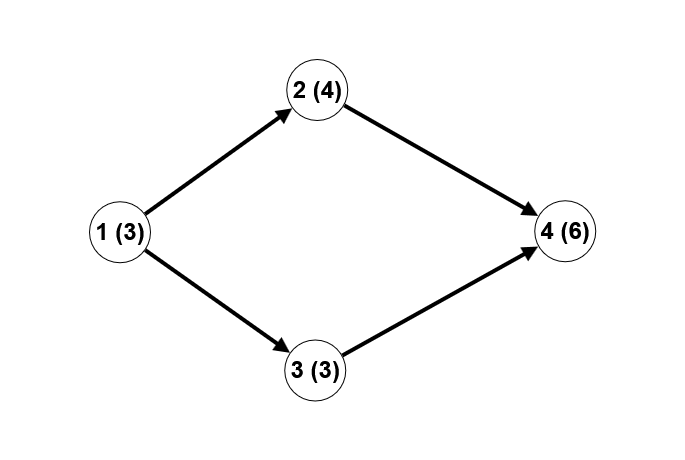
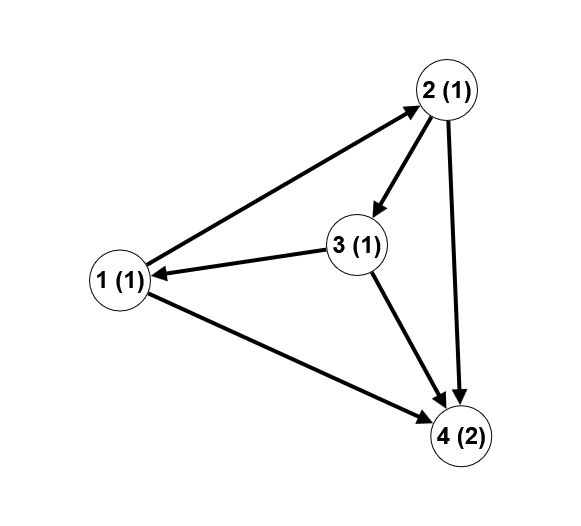
第一个样例的解释（顶点编号在括号外，顶点上的数字在括号内）：  本例中共有 5 条广义斐波那契路径：(1, 2), (1, 3), (2, 4), (3, 4), (1, 3, 4)。例如，路径 (1, 3, 4) 沿途顶点上的数字序列为：\[3, 3, 6\]，可以看到第三个数字等于前两个数字之和。 第二个样例的解释：  本例中共有 9 条广义斐波那契路径：(1, 2), (1, 4), (2, 3), (2, 4), (3, 1), (3, 4), (1, 2, 4), (2, 3, 4), (3, 1, 4)。注意，路径 (1, 2, 3) 上的数字序列为：\[1, 1, 1\]，这不是广义斐波那契数列。 由 ChatGPT 5 翻译