CF2178F Conquer or of Forest

定义有根树的独特装饰性染色如下： - 当以顶点 $v$ 为根的子树中的顶点个数是偶数时，将顶点 $v$ 染为白色； - 否则，将 $v$ 染成黑色。 在征服圣诞树森林的征途上，Yuuki 遇到了一棵已被装饰性染色的树 $T$，该树有 $n$ 个顶点，编号从 $1$ 到 $n$，根为顶点 $1$。 Yuuki 认为一棵树被征服当且仅当下列任一条件成立： - 树中不存在白色顶点，或 - 存在某个顶点 $v$，使得所有白色顶点都位于从根 $1$ 到 $v$ 的唯一路径上。 为了征服这棵树，Yuuki 可以任意次（也可以不做）进行如下操作： - 首先，选择一个染成白色且不是 $T$ 根的顶点 $w$。设 $p_w$ 是 $w$ 的父节点。 - 然后，移除连接 $p_w$ 和 $w$ 的边，并在任意两顶点间添加一条边，前提是 $T$ 依然是一棵树。 - 最后，重染 $T$ 使其满足装饰染色规则。注意，$T$ 总是以顶点 $1$ 为根。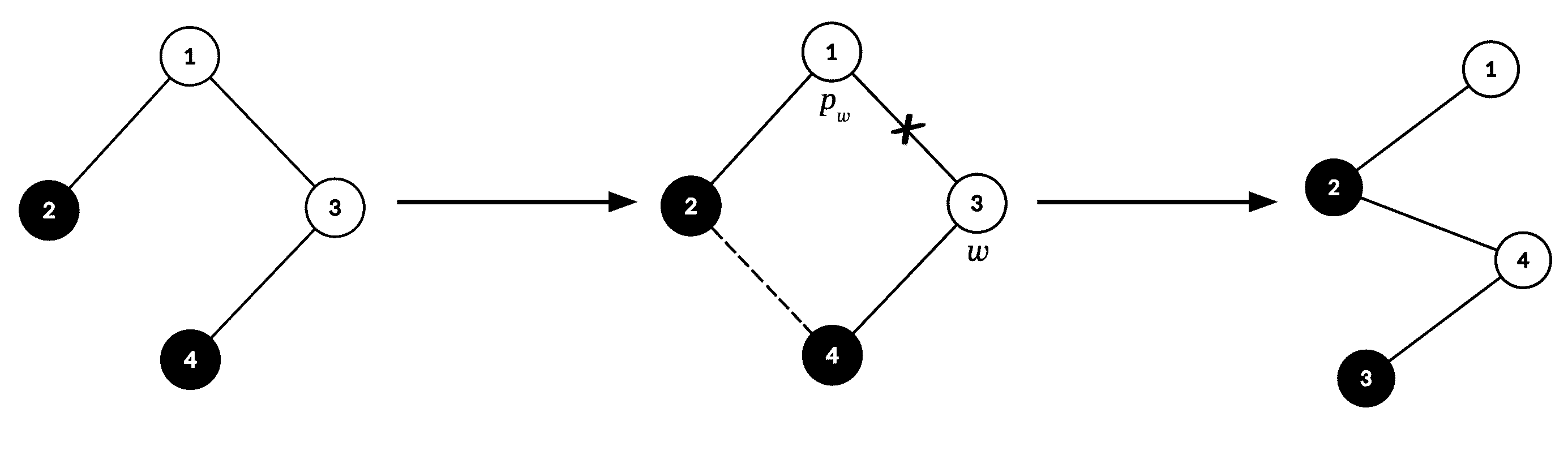  上图为第一组样例中操作的可能结果。生成的树被征服，因为所有白色顶点都在 $1$ 到 $3$ 的唯一路径上。 请计算通过任意次如上操作后，Yuuki 能够构造出的不同被征服树的数量。由于答案可能很大，请对 $998\,244\,353$ 取模输出。 注意，Yuuki 不能中途终止一次操作（特别是，他必须在判断前对树重新染色）。另外，即使树已经被征服，Yuuki 依然可以继续操作。 注解： - $^*$ 树是一个无环连通图。 - $^\dagger$ 顶点 $v$ 的子树是由 $v$ 及其所有后代和这些点之间的所有边组成的子图。 - $^\ddagger$ 只有当一对顶点在其中一棵树中有一条边、在另一棵树中没有这条边时，两棵树才被认为是不同的。

每组测试数据包含多组测试用例。第一行包含测试用例组数 $t$（$1 \le t \le 10^4$）。 每组测试数据第一行为一个整数 $n$（$2\le n\le 2\cdot 10^5$），表示 $T$ 的顶点数。 接下来 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1\le u_i

对于每个测试用例，输出一个整数，表示能够从 $T$ 构造出的不同被征服树的数量，对 $998\,244\,353$ 取模。

在第一个测试用例中，下列给出了能构造的四棵被征服树及其操作序列： 说明 | 插图 ------|----- - 零次操作。初始树已经被征服，因为所有白色顶点都在 $1$ 到 $4$ 的唯一路径上。 | 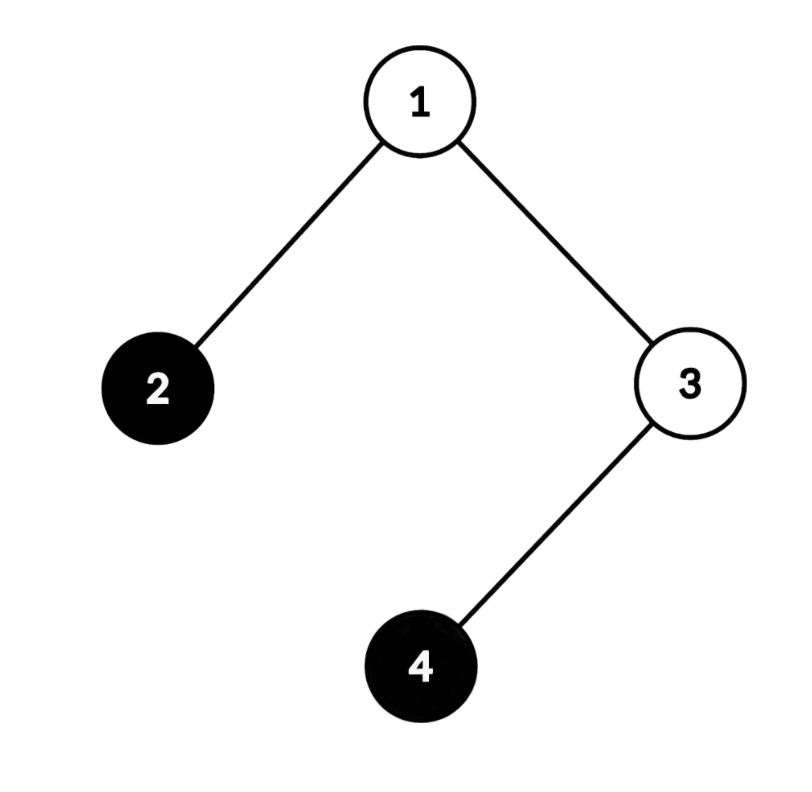 - 第一次也是唯一一次操作选择 $w=3$（$p_w=1$），在 $2$ 与 $4$ 之间连边。新树已被征服，因为所有白色顶点都在 $1$ 到 $3$ 的唯一路径上。 |  - 第一次也是唯一一次操作选择 $w=3$（$p_w=1$），在 $2$ 与 $3$ 之间连边。新树已被征服，因为所有白色顶点都在 $1$ 到 $3$ 的唯一路径上。 |  - 第一次操作选择 $w=3$（$p_w=1$），在 $2$ 与 $4$ 之间连边。第二次操作选择 $w=4$（$p_w=2$），在 $1$ 与 $4$ 之间连边。最终新树已被征服，因为所有白色顶点都在 $1$ 到 $4$ 的唯一路径上。 | 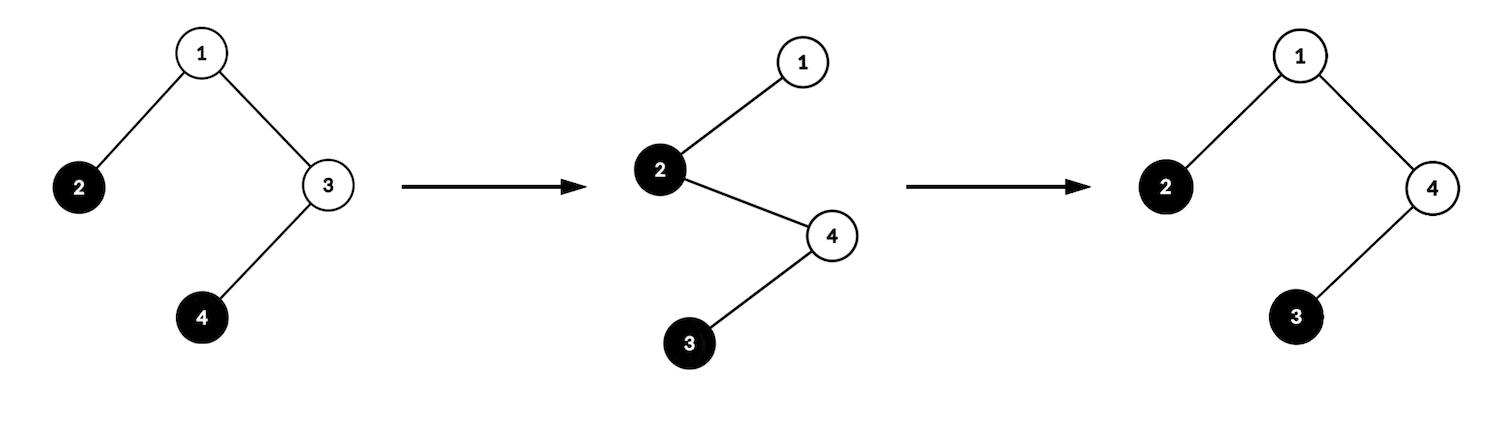 在第二组样例中，$T$ 不存在白色顶点，因此无法进行操作。而 $T$ 已经被征服，所以答案为 $1$。 由 ChatGPT 5 翻译