CF2178G deCH OR Dations

Due to supply chain issues in the North Pole (allegedly caused by a lazy elf), Santa is planning to give out hand-drawn circles as presents this Christmas. Please help him decorate them! There are $ 2n $ equally spaced points around the circle, labeled $ 1,2,\ldots,2n $ in clockwise order. Santa has chosen $ n $ chords with distinct endpoints, where chord $ i $ connects the points $ a_i $ and $ b_i $ . He draws these chords onto the circle one by one, in order. After Santa has drawn the first $ \ell $ chords, consider any non-empty subset $ S $ of the $ \ell $ chords and let $ 1\leq c_1

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2\le n\le 5\cdot 10^5 $ ) — the number of chords. Then $ n $ lines follow, the $ i $ -th line containing two integers $ a_i $ and $ b_i $ ( $ 1\le a_i

For each test case, output a string of length $ n $ — the $ \ell $ -th character should be $ \texttt{1} $ if the first $ \ell $ chords are tight-knit and $ \texttt{0} $ otherwise.

In the first test case, no pairs of chords intersect, and thus every chord appears in exactly one chain consisting of itself. Therefore, the chords are not tight-knit for all $ \ell $ . In the second test case, below is an illustration and explanation after the first $ \ell=1,2,3,4 $ chords are drawn. Sets of chords are denoted as a set of the indices of the corresponding chords. ExplanationIllustrationChains- $ \{1\} $ . Appearances- Chord $ 1 $ appears in $ 1 $ chain. Notes- The chords are not tight-knit since chord $ 1 $ is in an odd number of chains. - Recall that a set containing a single chord is always a chain. 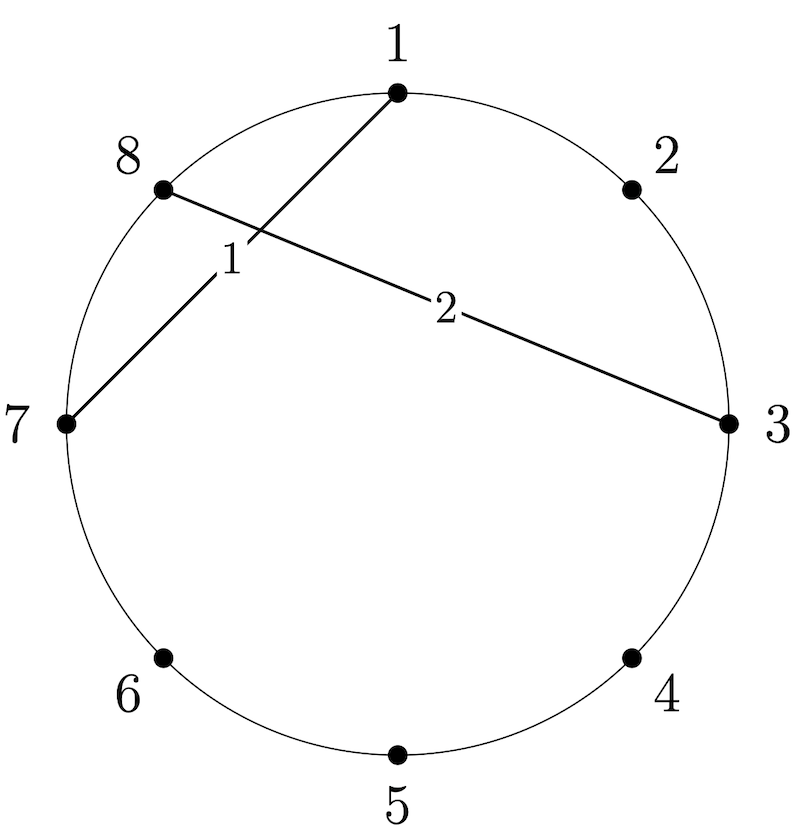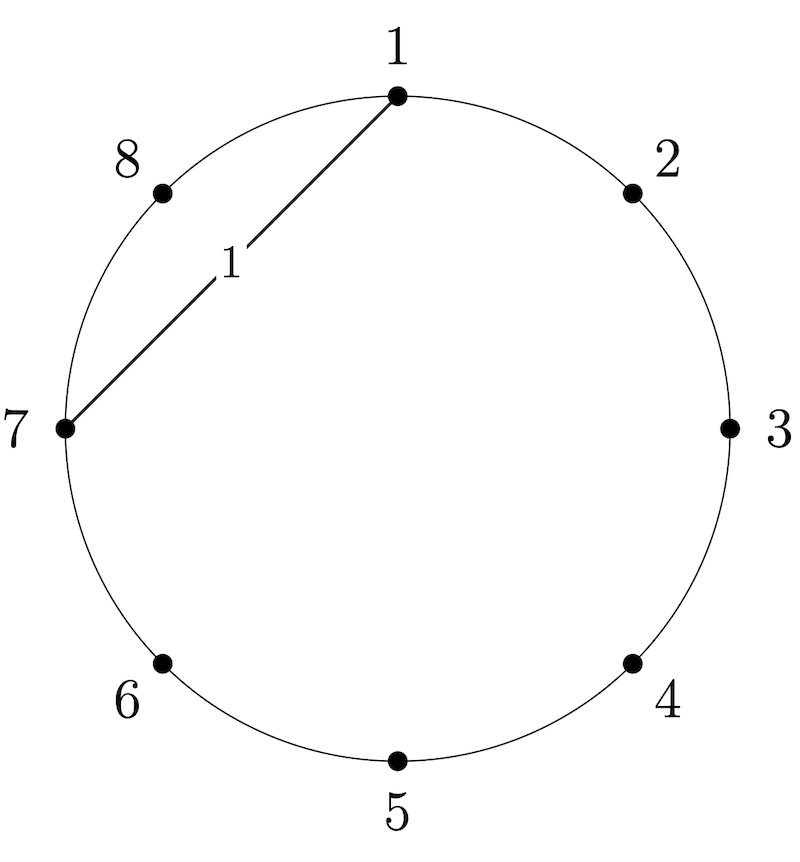Chains- $ \{1\} $ , $ \{1,2\} $ , and $ \{2\} $ . Appearances- Chord $ 1 $ appears in $ 2 $ chains; - Chord $ 2 $ appears in $ 2 $ chains. Notes- The chords are tight-knit since every chord appears in an even number of chains. 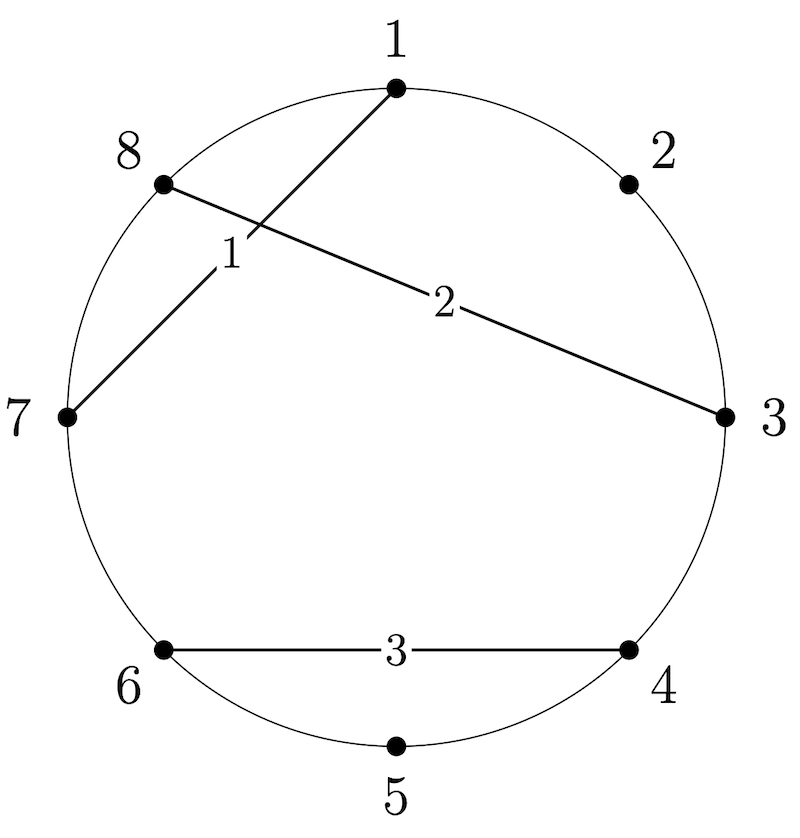Chains- $ \{1\} $ , $ \{1,2\} $ , $ \{2\} $ , and $ \{3\} $ . Appearances- Chord $ 1 $ appears in $ 2 $ chains; - Chord $ 2 $ appears in $ 2 $ chains; - Chord $ 3 $ appears in $ 1 $ chain. Notes- The chords are not tight-knit since chord $ 3 $ is in an odd number of chains. 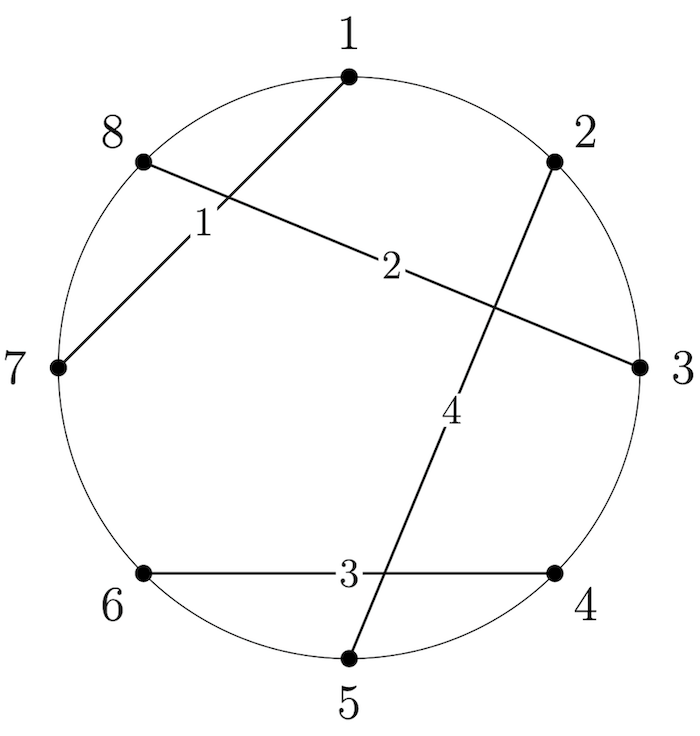Chains- $ \{1\} $ , $ \{1,2\} $ , $ \{1,2,4\} $ , $ \{2\} $ , $ \{2,4\} $ , $ \{3\} $ , $ \{3,4\} $ , and $ \{4\} $ . Appearances- Chord $ 1 $ appears in $ 3 $ chains; - Chord $ 2 $ appears in $ 4 $ chains; - Chord $ 3 $ appears in $ 2 $ chains; - Chord $ 4 $ appears in $ 4 $ chains. Notes- The chords are not tight-knit since chord $ 1 $ is in an odd number of chains. - Note that $ \{2,3,4\} $ is not a chain since chord $ 2 $ does not intersect chord $ 3 $ . Thus, we output $ \mathtt{0100} $ .