CF2178I Numbers or Fireworks

Now that all the presents have been delivered, the North Pole is finally at peace — and it's time to celebrate with a spectacular New Year's fireworks show! The North Pole is modeled as the Cartesian plane, with $ n $ cities located at distinct lattice points. You are also given an integer $ k $ . For a proper subset $ ^{\text{∗}} $ $ T $ of the cities ( $ T $ may be empty), we define its explosiveness as follows: 1. A firework is launched from every city in $ T $ . 2. For each city $ c $ not in $ T $ , let $ f $ be the number of fireworks launched from cities that are exactly $ \sqrt{k} $ Euclidean distance $ ^{\text{†}} $ away from $ c $ . Assign the number $ (f+1) $ to this city $ c $ . 3. The explosiveness of $ T $ is the product of all numbers assigned in Step 2. Compute the sum of the explosiveness of $ T $ over all $ 2^n-1 $ proper subsets $ T $ of the cities. Since the answer may be large, output it modulo $ 998\,244\,353 $ . $ ^{\text{∗}} $ A proper subset is any subset which is not equal to the whole set. $ ^{\text{†}} $ The Euclidean distance between two points $ (x, y) $ and $ (p, q) $ is defined as $ \sqrt{(x - p)^2 + (y - q)^2} $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 1000 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ k $ ( $ 2\le n\le 31 $ , $ 1\leq k \leq2\cdot 10^4 $ ). Then $ n $ lines follow, the $ i $ -th line containing two integers $ x_i $ and $ y_i $ ( $ 1\leq x_i, y_i\leq 100 $ ) — the $ x $ and $ y $ coordinates of the $ i $ -th city, respectively. It is guaranteed that the coordinates of the cities are pairwise distinct. It is guaranteed that the sum of $ n^3 $ over all test cases does not exceed $ 31^3 $ .

For each test case, print a single integer — the sum, modulo $ 998\,244\,353 $ , of the explosiveness over all proper subsets $ T $ of the cities.

In the first test case, below are the $ 2^3-1=7 $ possible placements of fireworks. The numbers assigned to cities not in $ T $ are circled. 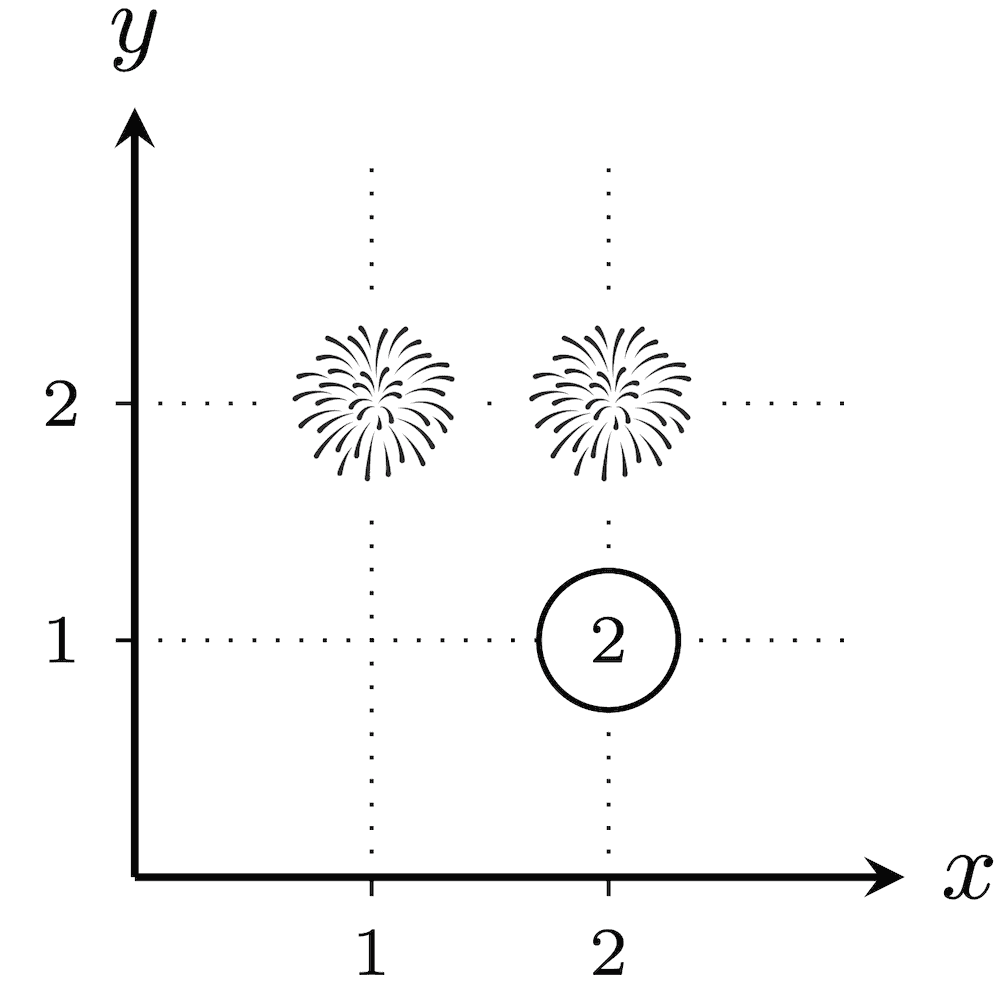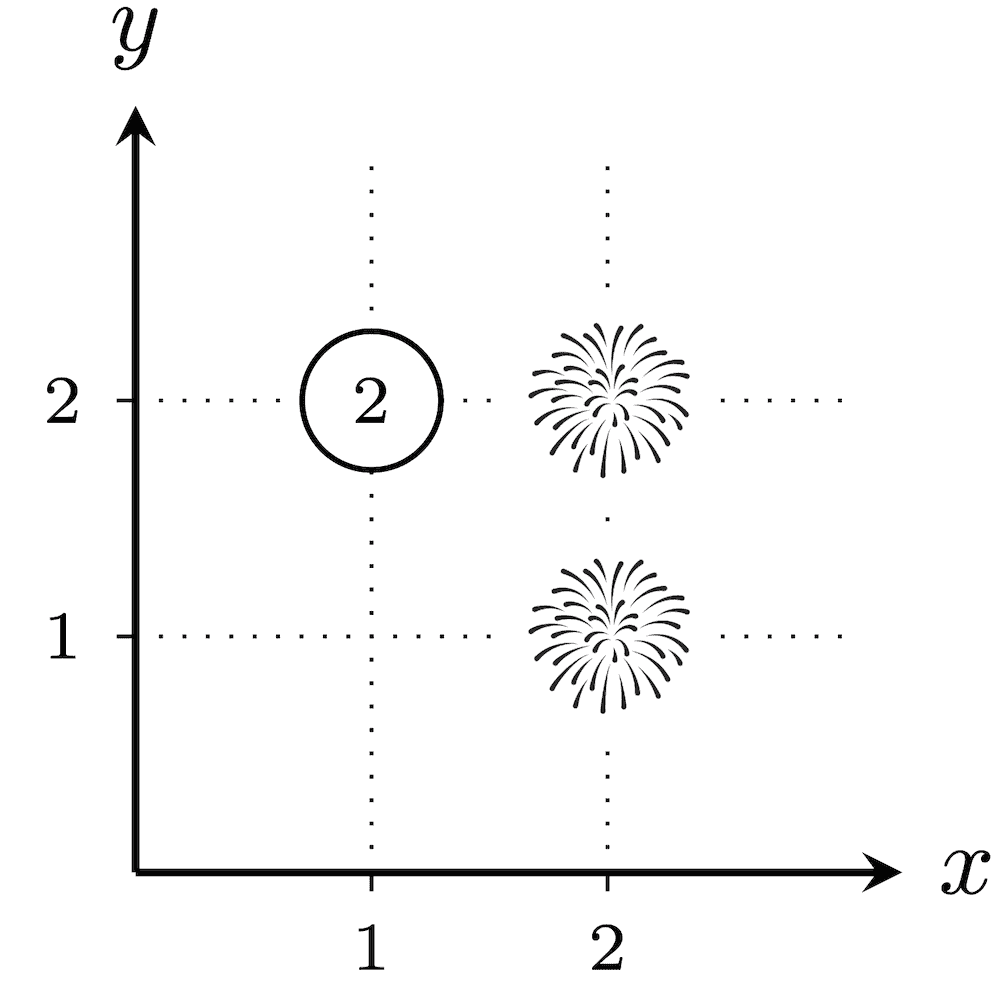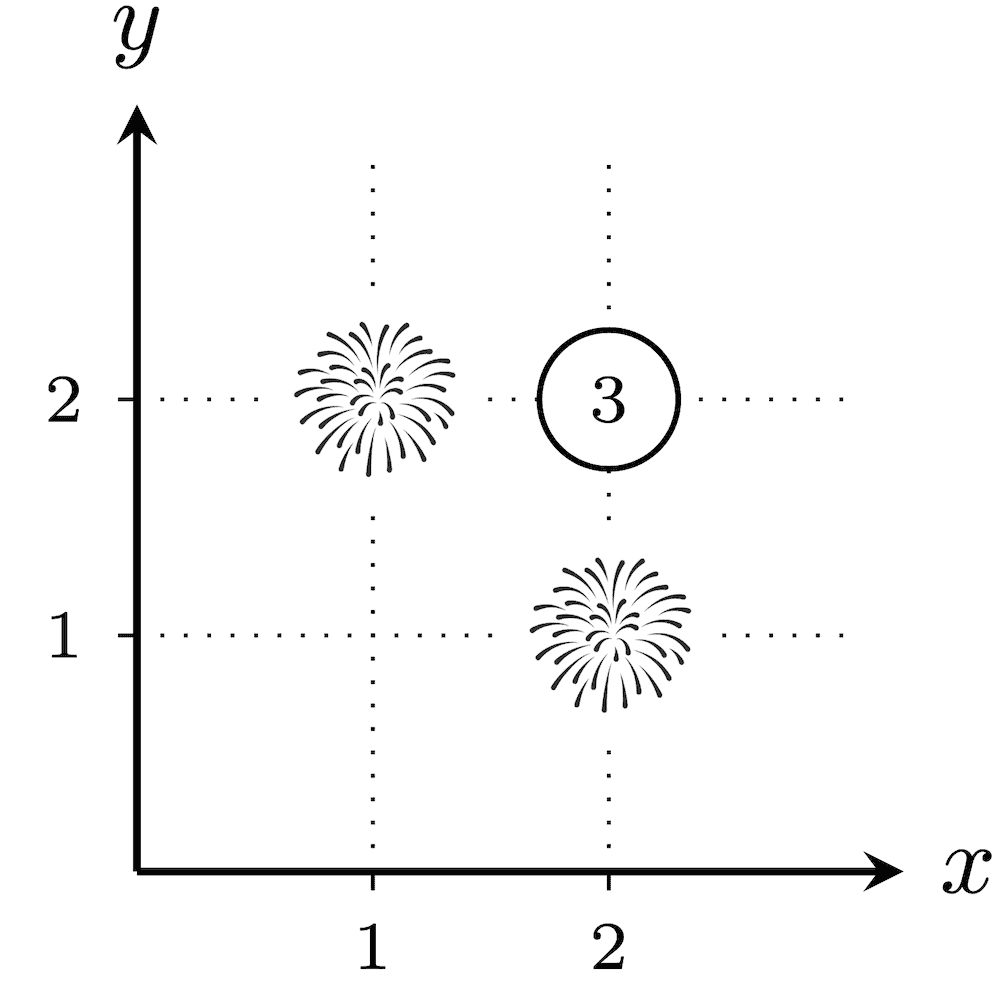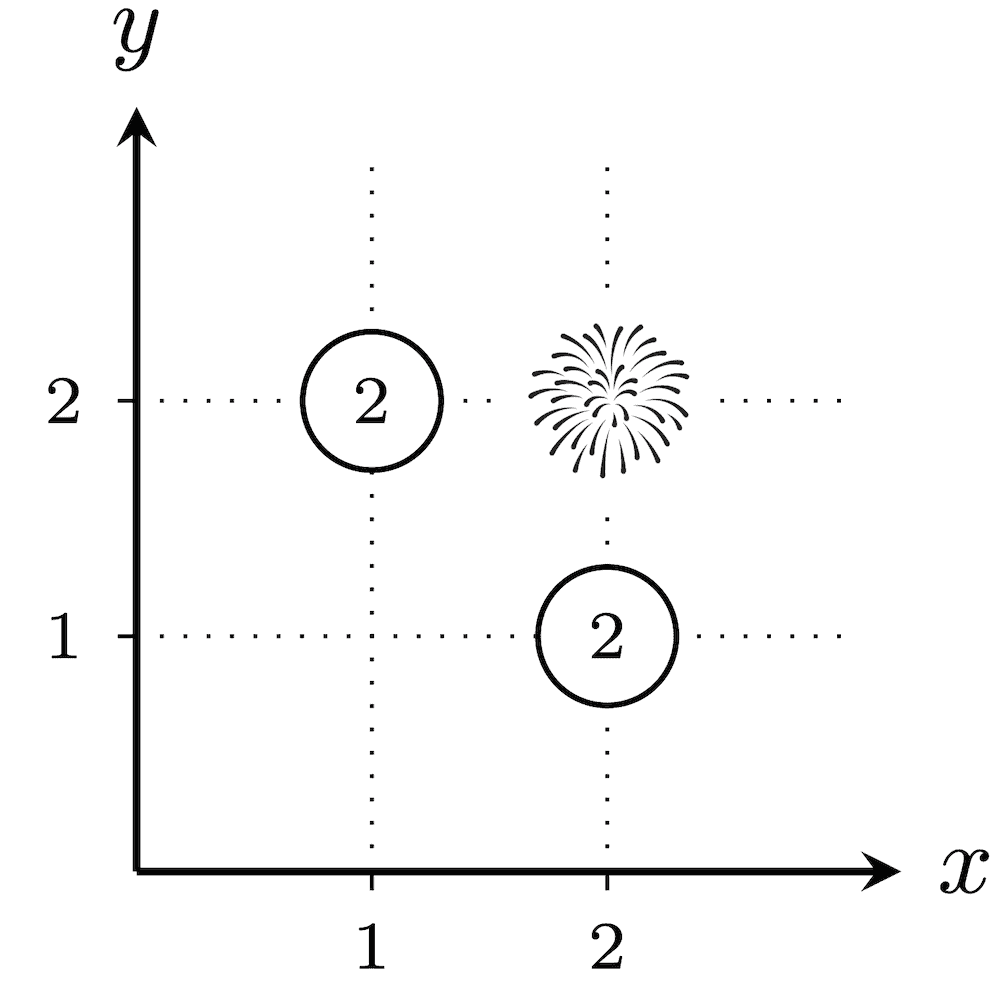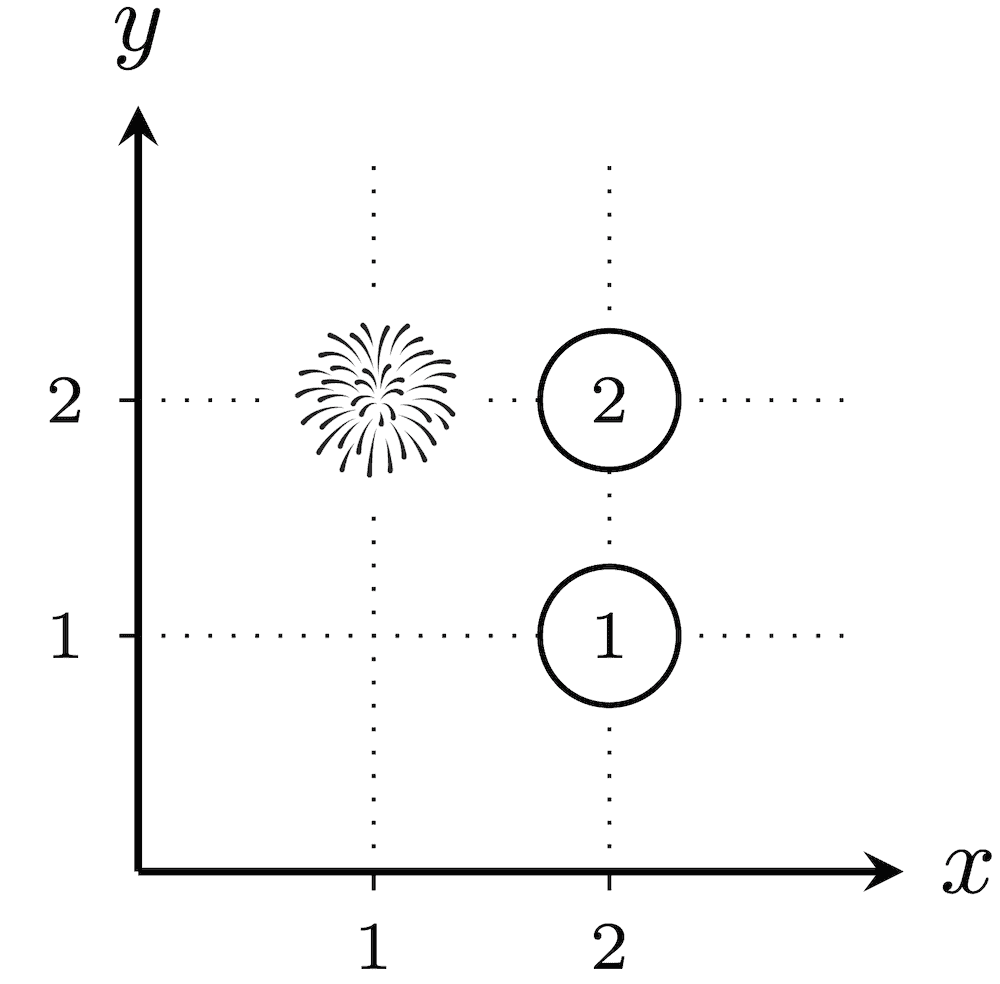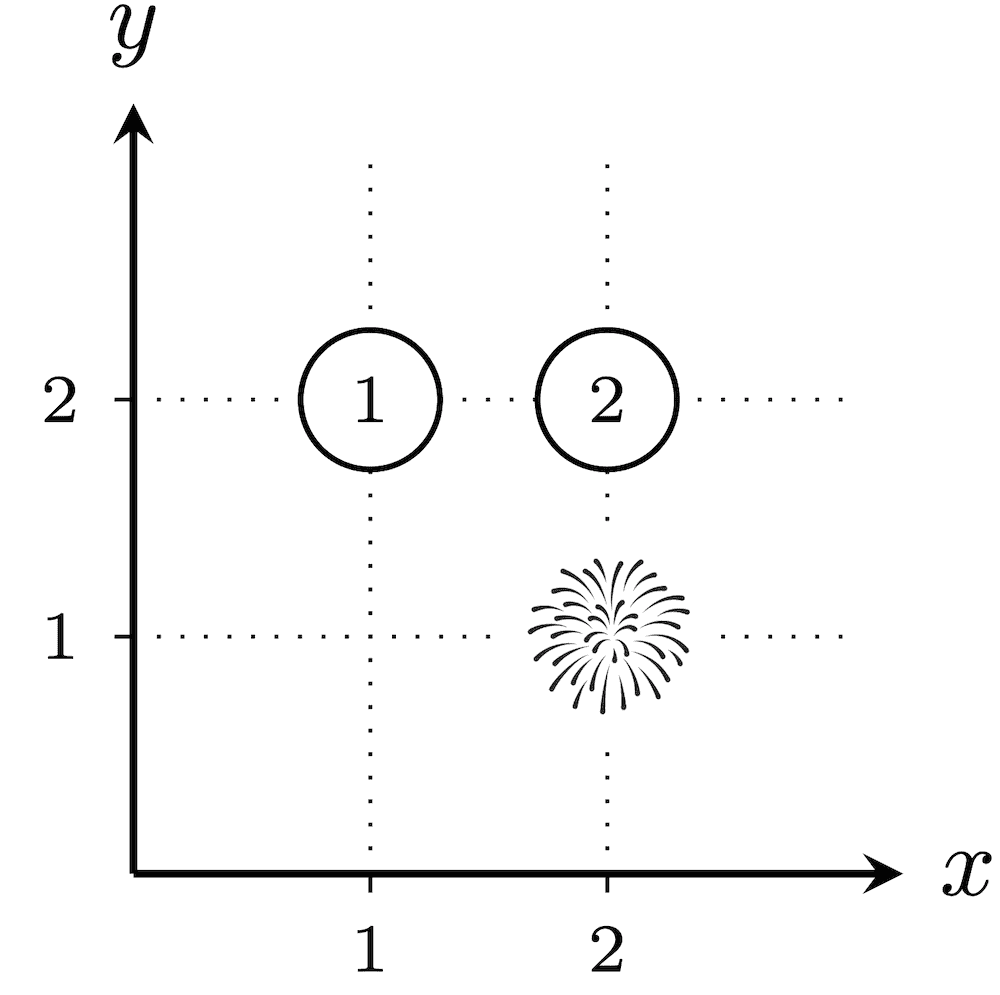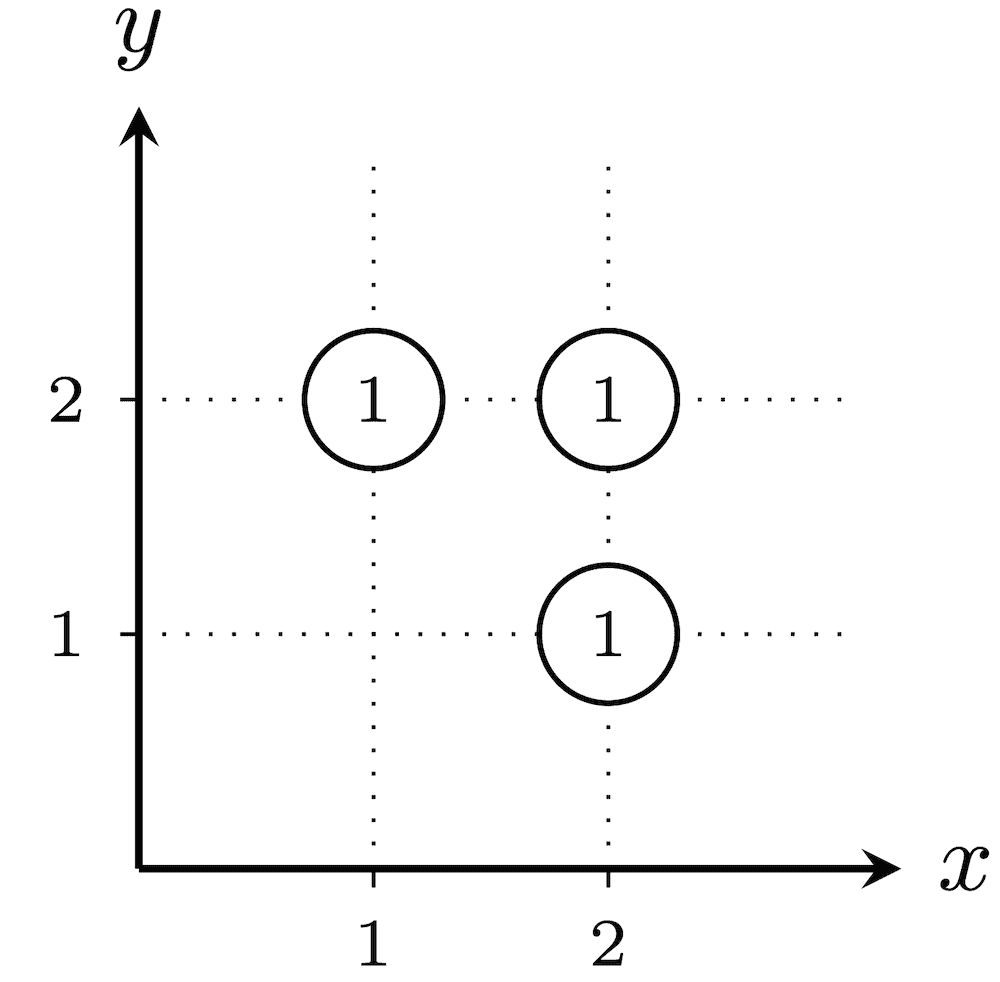 The total explosiveness is $ (1\cdot 1\cdot 1)+(1\cdot 2)+(2\cdot 1)+(2\cdot 2)+(3)+(2)+(2)=16 $ .In the second test case, there are $ 2^2-1=3 $ possible placements of fireworks. For every placement, since $ (1,1) $ and $ (100,100) $ have a Euclidean distance of $ \sqrt{(100-1)^2+(100-1)^2}=\sqrt{19\,602}\neq\sqrt{20\,000} $ , none of the cities will have fireworks that are exactly $ \sqrt{k} $ away. Thus, the number $ 1 $ is assigned to every city without fireworks. Therefore, the explosiveness is $ 1 $ for every $ T $ , and the answer is $ 1+1+1=3 $ .