CF2178I Numbers or Fireworks

现在所有礼物都已经送达，北极终于恢复了平静——是时候用一场壮观的新年烟花秀来庆祝了！ 北极被建模为一个平面直角坐标系，有 $n$ 个城市分别位于不同的整点上。你还得到了一个整数 $k$。 对于城市集合的任意一个真子集 $^{\text{∗}}$ $T$（$T$ 可以为空），我们这样定义其爆炸性： 1. 每个在 $T$ 中的城市发射一枚烟花。 2. 对于每个不属于 $T$ 的城市 $c$，记 $f$ 为距离 $c$ 恰好为 $\sqrt{k}$ 的烟花发射城市的数量。给该城市 $c$ 赋值 $(f+1)$。 3. $T$ 的爆炸性为步骤 2 中所有被赋值城市数值的乘积。 请你计算所有 $2^n-1$ 个非全集真子集 $T$ 的爆炸性之和。由于答案可能非常大，请输出答案对 $998\,244\,353$ 取模后的结果。 $^{\text{∗}}$ 真子集定义为严格小于全集的子集（即不是全集本身）。 $^{\text{†}}$ 两点 $(x, y)$ 和 $(p, q)$ 之间的欧几里得距离定义为 $\sqrt{(x-p)^2 + (y-q)^2}$。

每组测试数据包含多组测试用例。第一行包含测试用例组数 $t$（$1 \le t \le 1000$）。接下来 $t$ 组数据，每组描述如下： 每组数据的第一行包含两个整数 $n$、$k$（$2 \le n \le 31$，$1 \leq k \leq 2 \cdot 10^4$）。 接下来 $n$ 行，每行两个整数 $x_i$ 和 $y_i$（$1 \leq x_i, y_i \leq 100$），表示第 $i$ 个城市的横纵坐标。保证城市间的坐标各不相同。 保证所有测试用例的 $n^3$ 之和不超过 $31^3$。

对于每个测试用例，输出一个整数，表示所有真子集 $T$ 的爆炸性之和，对 $998\,244\,353$ 取模后的结果。

在第一个测试用例中，所有 $2^3 - 1 = 7$ 种烟花发射方案如下。未被选中发射烟花的城市，其被分配的数值圈出表示。 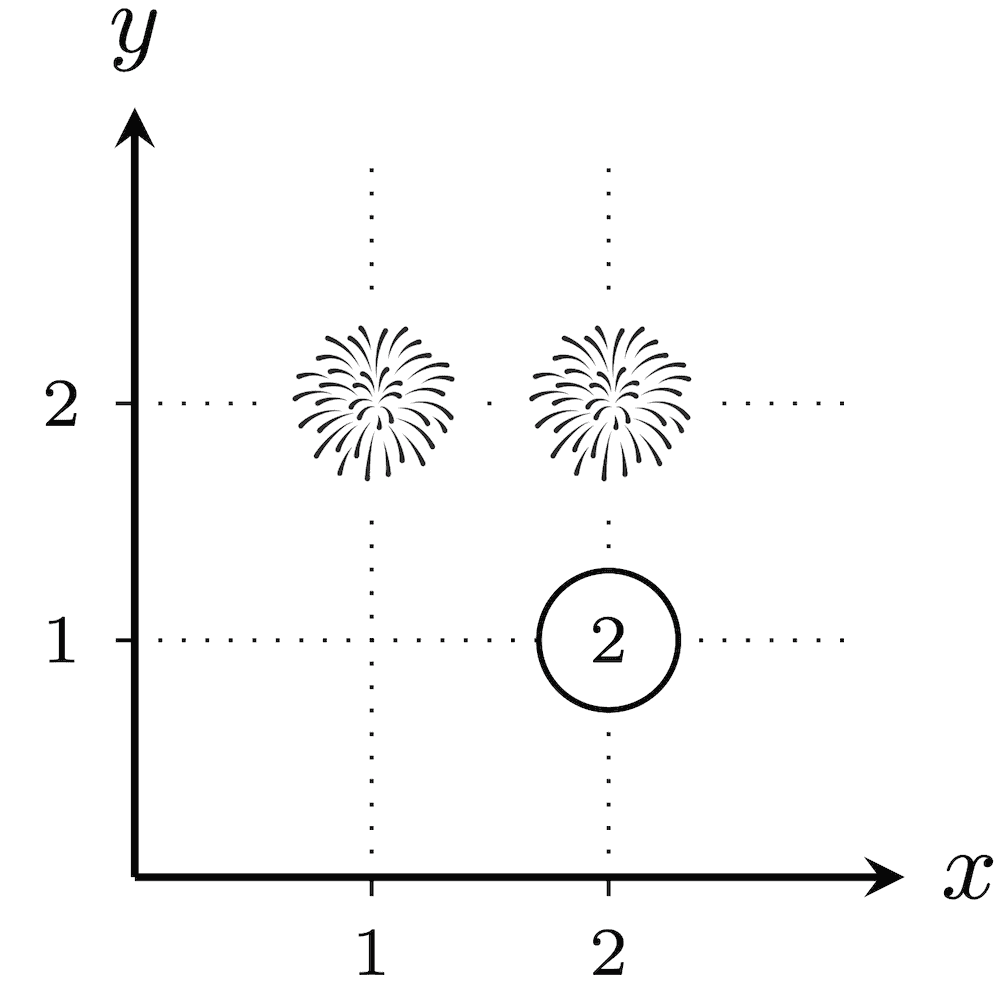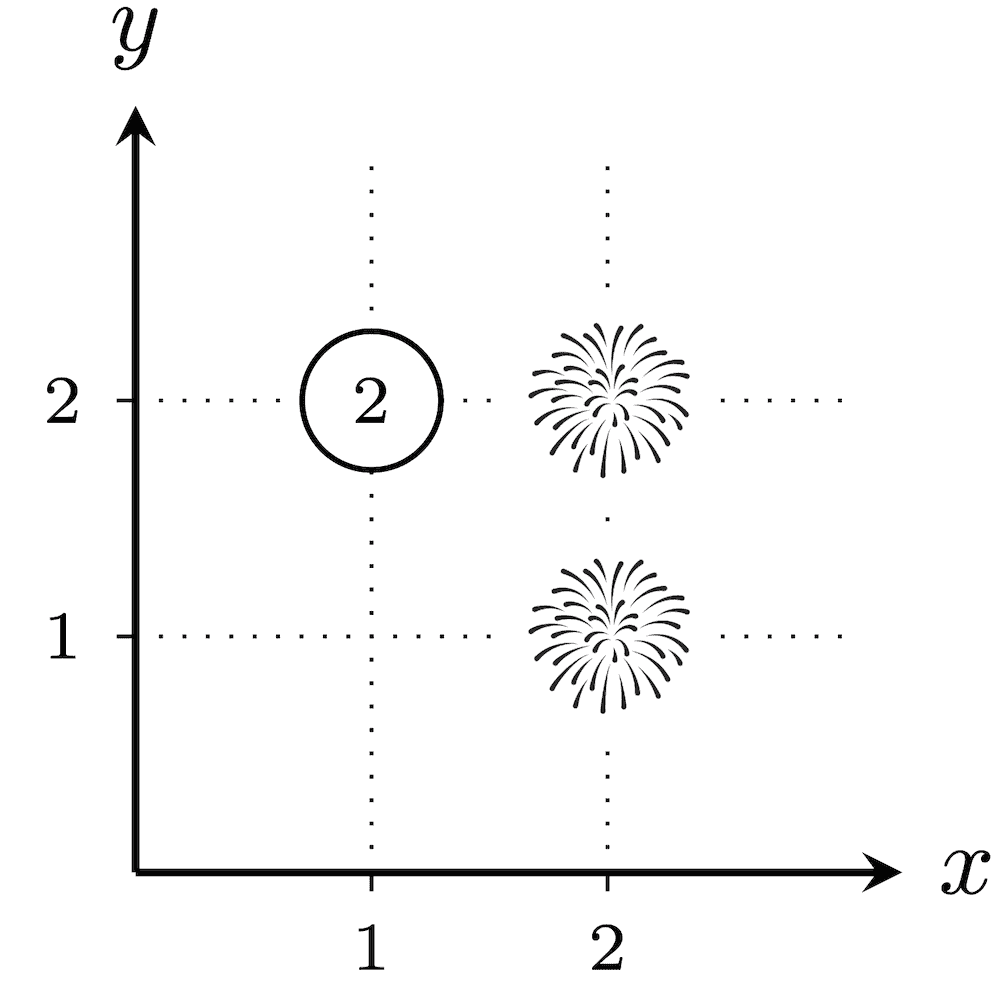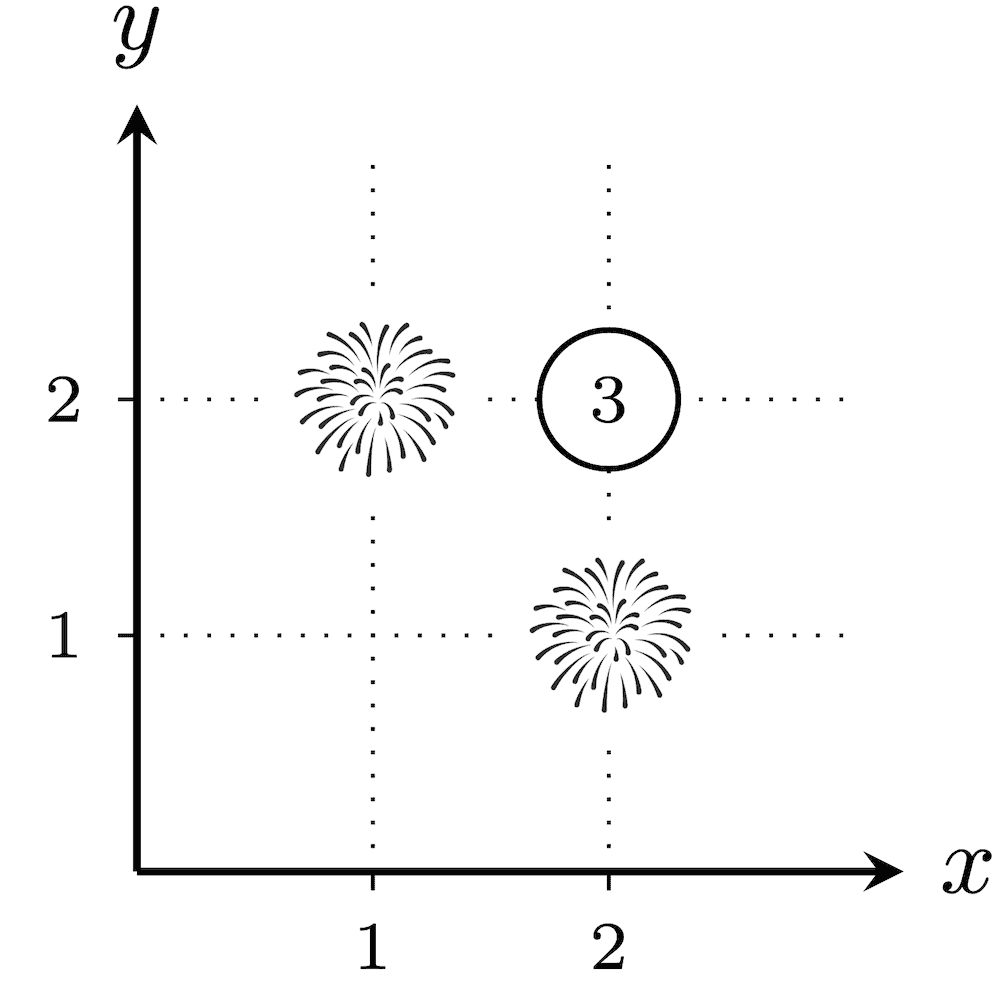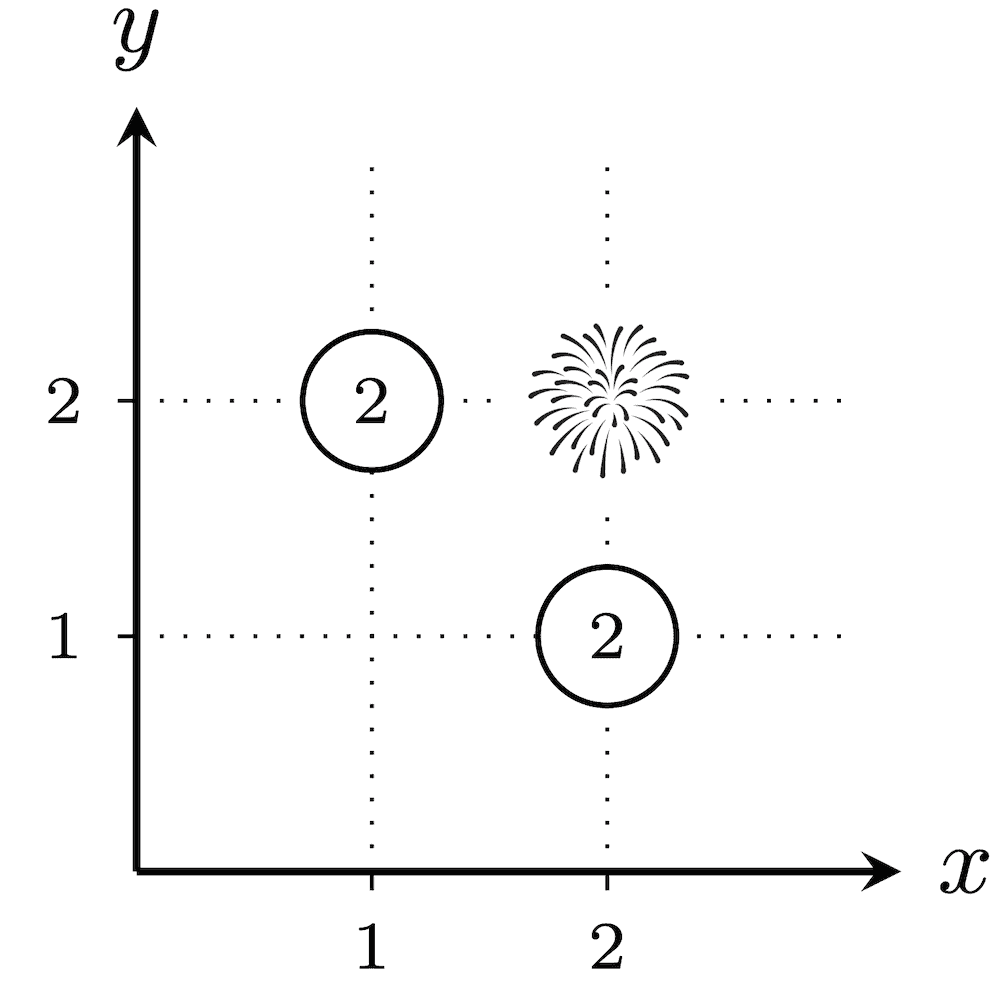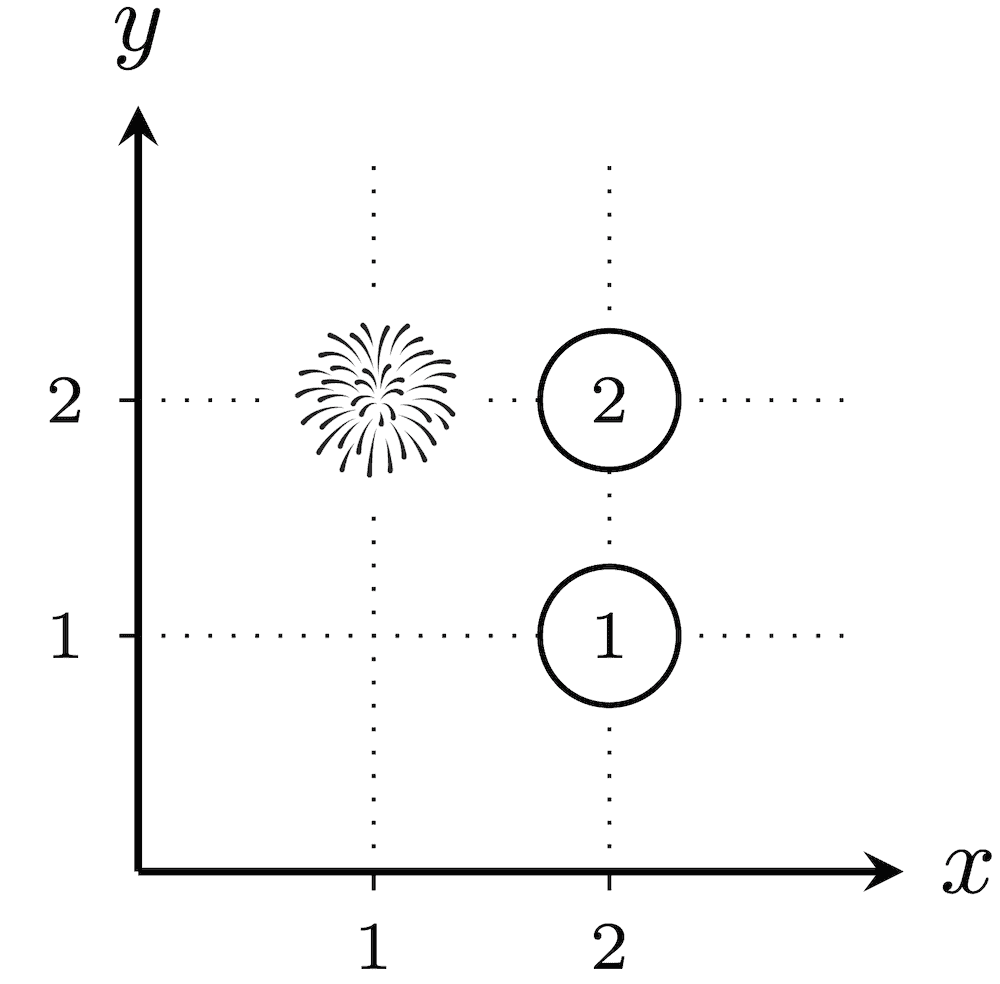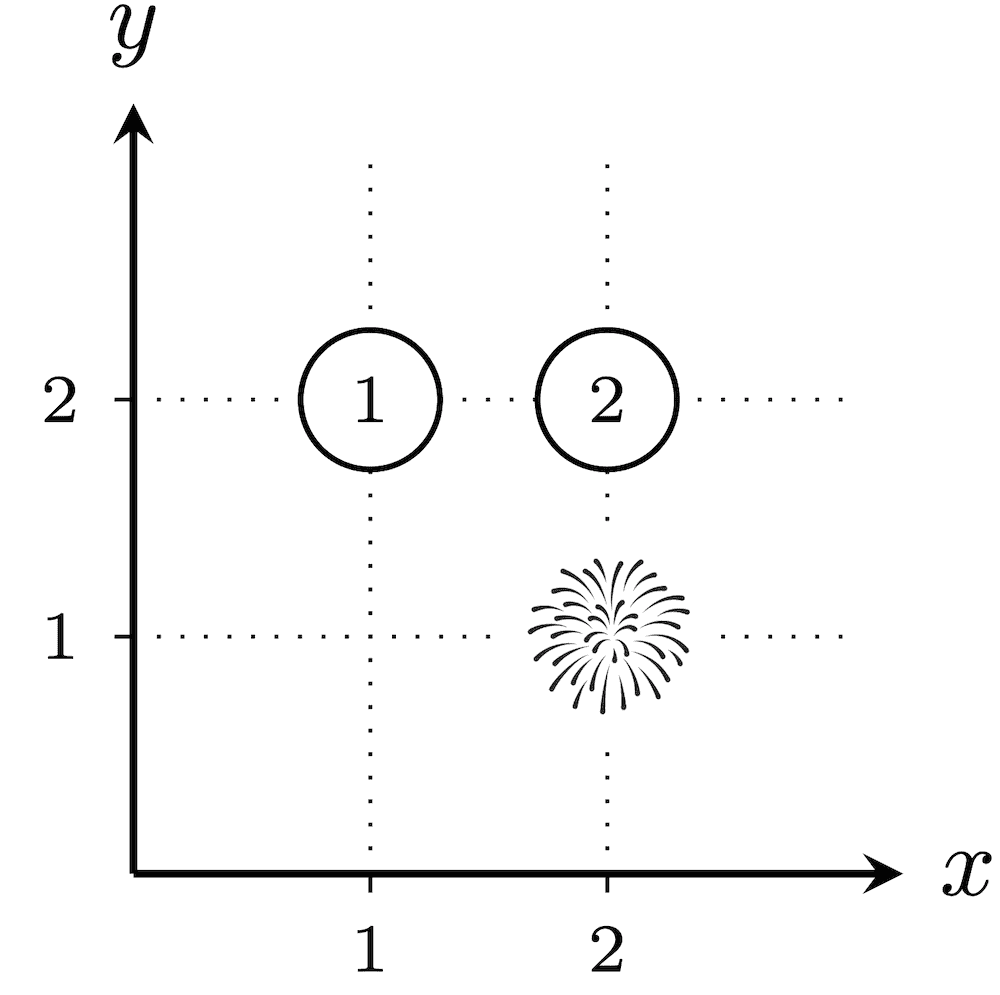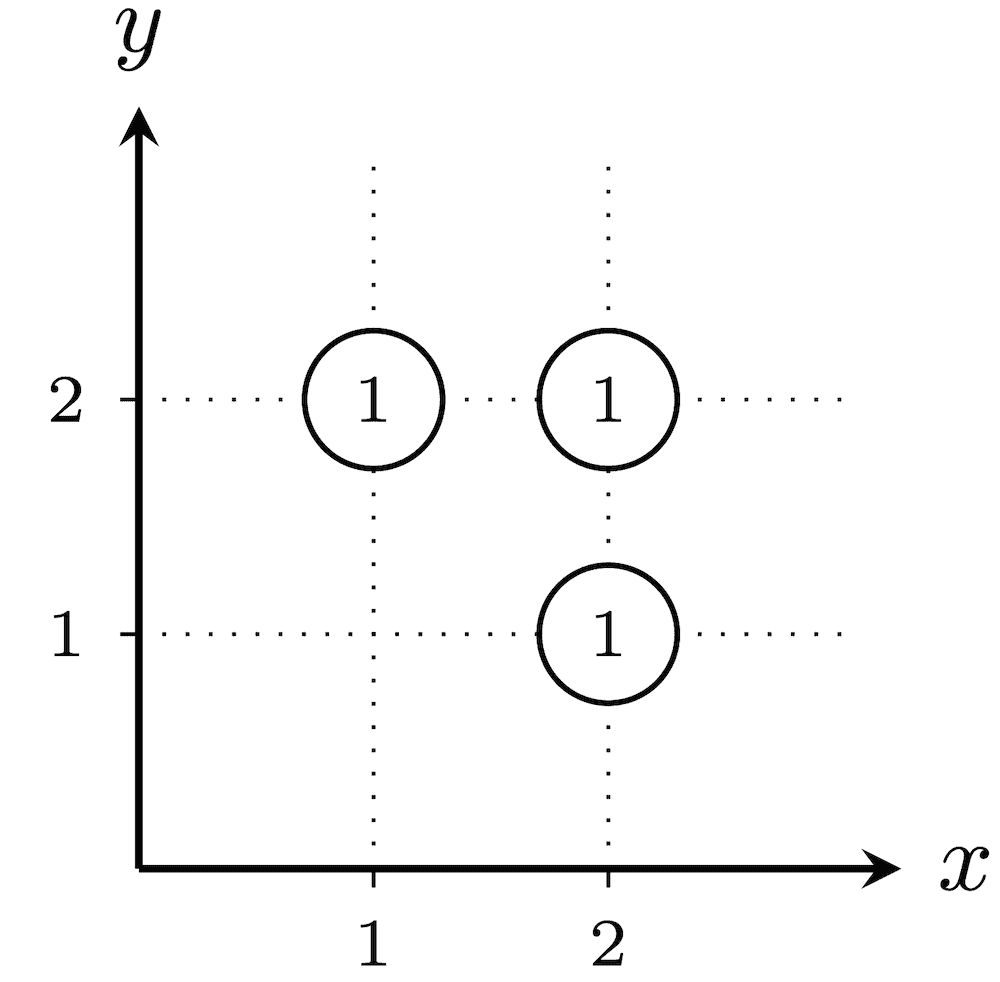 总爆炸性为 $(1 \cdot 1 \cdot 1)+(1 \cdot 2)+(2 \cdot 1)+(2 \cdot 2)+(3)+(2)+(2)=16$。 在第二个测试用例里，共有 $2^2-1=3$ 种烟花发射方式。任意一种方案，从 $(1,1)$ 到 $(100,100)$ 的欧几里得距离为 $\sqrt{(100-1)^2+(100-1)^2}=\sqrt{19\,602}\neq\sqrt{20\,000}$，不存在距离恰好为 $\sqrt{k}$ 的城市，所以每个没放烟花的城市都会被分配数值 $1$。因此，每种真子集 $T$ 的爆炸性均为 $1$，所以答案为 $1+1+1=3$。 由 ChatGPT 5 翻译