CF2180D Insolvable Disks
题目描述
在平面 $X$ 轴上给定 $n$ 个不同的整点 $x_1 < x_2 < \ldots < x_n$。对于每个 $1 \leq i \leq n$,你需要选择一个实数 $r_i > 0$,并以 $x_i$ 为圆心、$r_i$ 为半径画一个圆盘,使得任意两个圆盘都不重叠。
你希望选择 $r_i$ 的方式,使得圆盘之间互相外切的对数最大,并求出这个最大值。
我们认为,如果两个圆盘的交集面积为正,则它们重叠。特别地,如果两个圆盘恰好外切,则它们不重叠。
输入格式
每组测试包含若干测试用例。第一行包含一个整数 $t$($1 \leq t \leq 10^4$),表示测试用例的数量。
每个测试用例的第一行包含一个整数 $n$($1 \leq n \leq 2\cdot 10^6$)——该测试用例中点的数量。
每个测试用例的第二行包含 $n$ 个整数 $x_1, x_2, \ldots, x_n$($0 \leq x_1 < x_2 < \ldots < x_n \leq 10^9$),表示这些点的坐标。
保证所有测试用例中 $n$ 的总和不超过 $2\cdot 10^6$。
输出格式
对于每组测试用例,输出一个整数,表示该测试用例中最多能得到多少对外切的圆盘。
说明/提示
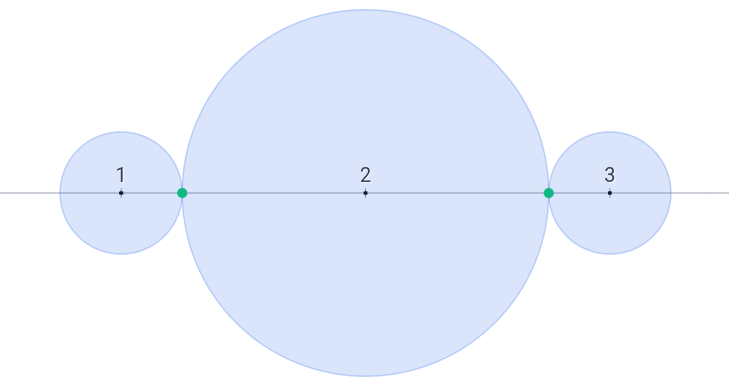
在第一个测试用例中,可以取 $r_1 = r_3 = 0.25$,$r_2 = 0.75$,则第 $1$、$2$ 个圆盘以及第 $2$、$3$ 个圆盘两两外切。
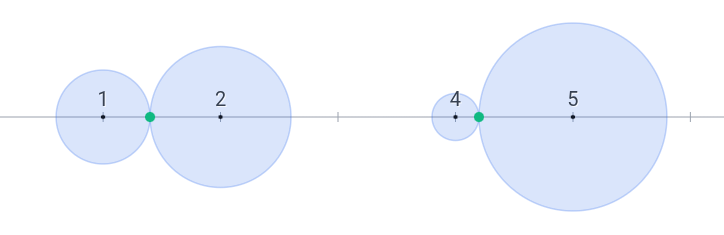
在第二个测试用例中,可以取 $r_1 = 0.4$,$r_2 = 0.6$,$r_3 = 0.2$,$r_4 = 0.8$,则第 $1$、$2$ 个圆盘以及第 $3$、$4$ 个圆盘两两外切。
在第三个测试用例中,最优解是让每个 $r_i = 0.5$,第 $1$ 和 $2$,$3$ 和 $4$,$5$ 和 $6$ 组成为外切圆盘对。
[可视化工具链接](https://codeforces.com/assets/contests/2180/D_uZiePo9ziin2eish5yai.html)
由 ChatGPT 5 翻译