CF2180F2 Control Car (Hard Version)

这两个版本的区别在于限制条件，包括变量的取值范围、时间和内存限制。仅当你同时解决了本题目的两个版本时，才可以进行 hack。请注意，困难版本的正确解未必是简单版本的有效解。 我们有一辆“控制小车”，它的行为类似于一个随机变量。正如随机变量既不是真正随机，也不是真正变量，我们的“控制小车”既不是汽车，也不可控！ 无论如何，给定一个 $n \times m$ 的网格，这个网格由 $n+1$ 条水平线和 $m+1$ 条竖直线交叉组成。网格包含 $(n+1)(m+1)$ 个交点，这些交点是单元格四周的角。 一种“朝向”是给每个交点分配一个四个基本方向（上、下、左、右）中的一个。因此，总共有 $4^{(n+1)(m+1)}$ 种可能的朝向方案。 对于一种朝向，请按如下流程操作： 1. 对于网格上的每个点，从该点按分配的方向画出一堵单位长度的墙。墙壁可能会重叠或伸出网格边界之外。 2. 将控制小车放在左上角的单元格 $(1,1)$。然后，只要小车没有停止，它就会按照这些规则移动： - 如果小车可以向下移动（即向下到达正下方单元格的路径没有被墙堵住），则它会因重力向下移动。 - 如果它不能向下移动但可以向右移动（即通向右侧相邻单元格的路径没有被墙堵住），则它会向右移动。 - 如果小车移动出网格或无法移动，则停止。 3. 如果控制小车最终停在网格内部，则该朝向方案是合法的。 请计算所有合法朝向的数量。由于答案可能非常大，请输出其对 $10^9+7$ 取模后的结果。

每组测试数据包含多个测试用例。第一行为测试用例个数 $t$（$1 \le t \le 50$）。每个测试用例描述如下。 每个测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \le n \le \mathbf{50}$，$1 \le m \le \mathbf{10^{15}}$），表示网格的大小。 所有测试用例中 $n$ 的总和不超过 $\mathbf{50}$。

对于每个测试用例，输出合法朝向的数量，对 $10^9+7$ 取模后的结果。

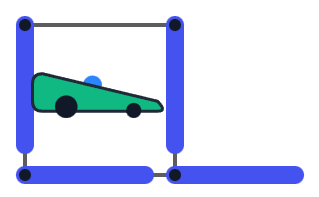
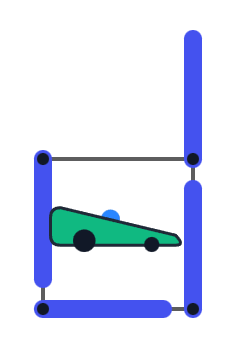
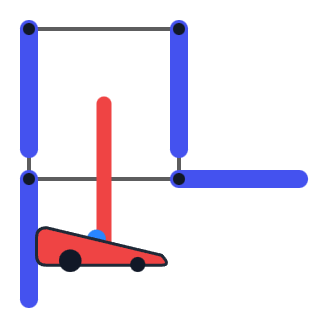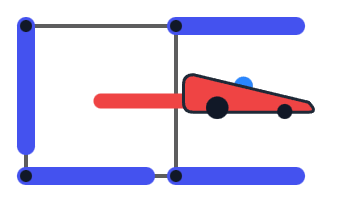
在第一个测试用例中，要使某个朝向合法，至少需要左下角或右下角的墙壁覆盖网格的下边界。同时还需要右上角或右下角的墙壁覆盖网格的右边界。如果这两个条件都满足，则该朝向为合法朝向。 现在，如果右上角朝下、左下角朝右，则左上角和右下角可以指向任意方向。因此，此类情况有 $16$ 种合法朝向。  第一个类型的合法朝向示意图。如果右上角或左下角指向不同方向，则右下角必须覆盖对应的边界。因此，只有其中一个可以指向不同方向。总共有 $2 \cdot 3 \cdot 4 = 24$ 种此类合法朝向。  第二种类型的合法朝向示意图。因此，最终答案是 $16+24=40$。   两个非法朝向的示例。 [可视化工具链接](https://codeforces.com/assets/contests/2180/F_eegai9Doo0heequiev6e.html) 由 ChatGPT 5 翻译