CF2181C Cacti Classification

Ivan and Petr like to play with cacti — special graphs where each edge belongs to at most one simple cycle, and the graph is connected. Multiple edges between pairs of vertices and loops are allowed. They invent the following game: - Petr secretly builds a cactus with $ n $ vertices and $ m $ edges. The edges are labeled from $ 1 $ to $ m $ . - Petr only tells Ivan the number $ m $ . - Ivan is then allowed to ask questions of the following form: - He chooses a subset $ S $ of edge labels (see below about limitations on the subset), and asks: "If we only keep the edges whose labels are in $ S $ (and all $ n $ vertices), is the resulting graph connected?" - Petr must answer either "yes" or "no". After asking at most $ 8m $ questions, Ivan must determine, for every edge: 1. whether this edge lies on some cycle in the cactus; 2. if it does, what is the length of that simple cycle. In this problem, each loop is considered a simple cycle of length $ 1 $ and two edges between the same pair of vertices form a simple cycle of length $ 2 $ . However, Ivan is still very young and only knows numbers up to $ 14 $ . So: - if an edge lies on a simple cycle of length at most $ 14 $ , he must output that exact length; - if an edge lies on a simple cycle of length greater than $ 14 $ , he must say that this edge lies on a big cycle. Also, to avoid having to list a lot of edges each time, Ivan always asks about an edge set obtained from the set used in one of the previous queries, or from the set of all edges, by removing exactly one edge. Can you design a strategy that allows Ivan to complete this task?

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). The description of the test cases follows. The first line of each test case contains $ m $ ( $ 1 \le m \le 10^4 $ ) — the number of edges in the cactus. It is guaranteed that the sum of $ m $ over all test cases does not exceed $ 10^4 $ .

N/A

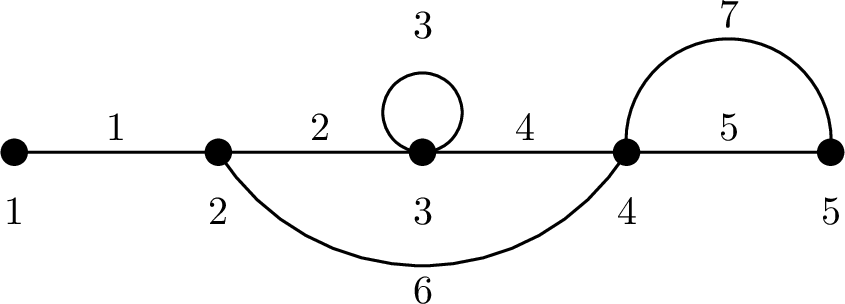
In the example interaction, the input and output contain empty lines to align interactor responses with queries. These empty lines do not appear in the actual input and output. In this example, the graph has $ 5 $ vertices and $ 7 $ edges; edges $ 1 $ through $ 7 $ , in this order, are $ (1, 2) $ , $ (2, 3) $ , $ (3, 3) $ , $ (3, 4) $ , $ (4, 5) $ , $ (2, 4) $ , $ (4, 5) $ .