CF2181C Cacti Classification
题目描述
Ivan 和 Petr 喜欢玩仙人掌(一种特殊的图,每条边至多属于一个简单环,并且图是连通的)。允许多重边和自环。
他们发明了如下游戏:
- Petr 秘密构造一个有 $n$ 个顶点和 $m$ 条边的仙人掌。边按照 $1$ 到 $m$ 编号。
- Petr 只告诉 Ivan 边的数量 $m$。
- 然后,Ivan 可以反复提如下类型的问题:
- 他选择一个边的编号子集 $S$(关于子集的限制见下文),并提问:“如果我们只保留编号在 $S$ 中的边(以及所有 $n$ 个顶点),结果图是连通的吗?”
- Petr 必须回答“是”或“否”。
Ivan 最多只能提 $8m$ 个问题,便必须判定每一条边:
1. 这条边是否属于某个环;
2. 如果属于,需要指出该简单环的长度。
本题中,每个自环看作长度为 $1$ 的简单环,两个同一顶点对间的边组成长度为 $2$ 的简单环。
然而,Ivan 年纪尚小,只认识 $14$ 以内的数。因此:
- 如果某条边属于长度不超过 $14$ 的简单环,他必须输出准确的长度;
- 如果环的长度超过 $14$,则输出该边属于大环。
此外,为避免每次操作都需列出繁琐的边集,Ivan 的每个询问都要求如下:询问的边集需由上一次已用的边集,或由全体边集,通过删去恰好一条边得到。
请设计一种策略,使 Ivan 能完成任务。
输入格式
每组测试包含多个测试用例。第一行包含测试用例数 $t$($1 \le t \le 100$)。每组测试用例描述如下。
每组测试用例首行为 $m$($1 \le m \le 10^4$),表示仙人掌的边数。
保证所有测试用例中 $m$ 的总和不超过 $10^4$。
输出格式
(交互题,输出格式参见题目原文,略。)
说明/提示
在样例交互中,为对齐交互器响应与询问,输入输出中出现了空行。实际输入输出不会有这些空行。
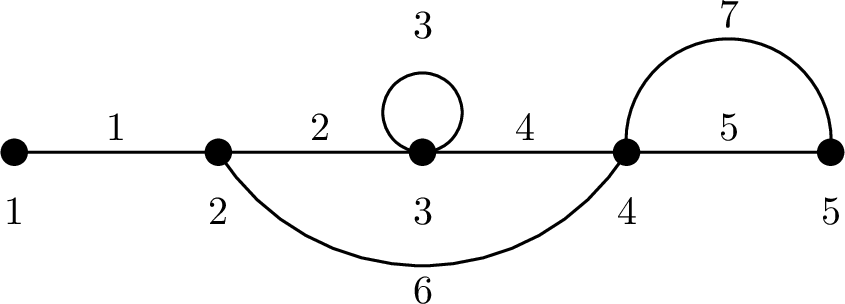
样例中,图有 $5$ 个顶点和 $7$ 条边;编号 $1$ 到 $7$ 的边分别为 $(1,2)$,$(2,3)$,$(3,3)$,$(3,4)$,$(4,5)$,$(2,4)$,$(4,5)$。
由 ChatGPT 5 翻译