CF2181H Honey Cake

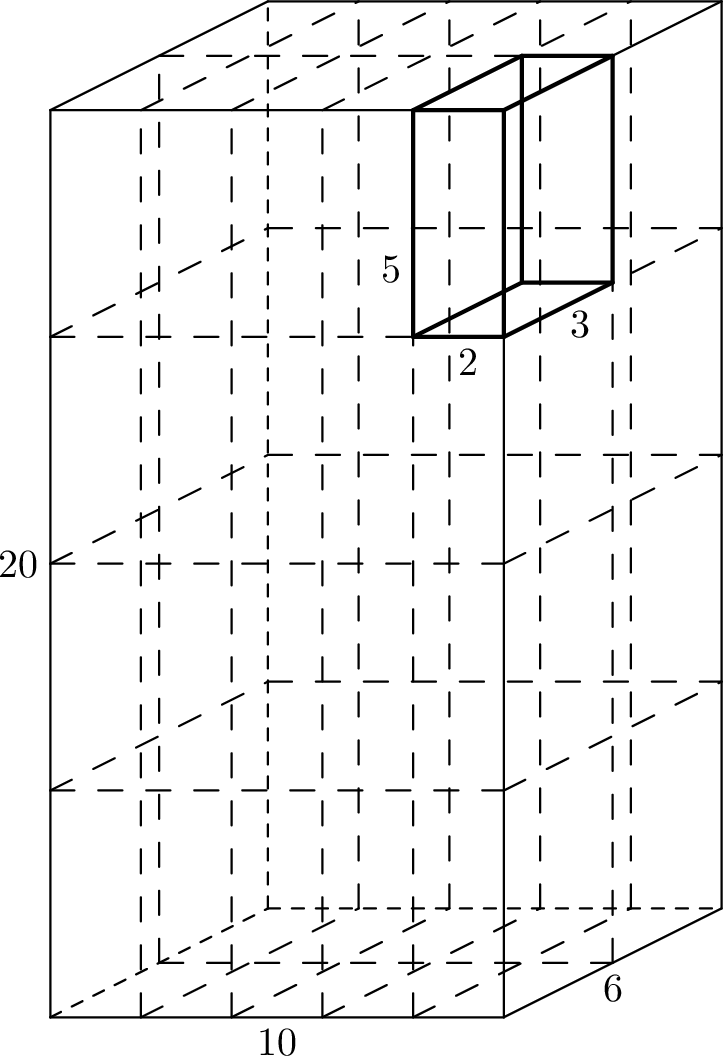
Hannah and Henry are going to host a party for $ n $ people, including themselves. They bought a honey cake of size $ w \times h \times d $ inches for the party, and want to split it into $ n $ equal pieces. The honey cake can be cut parallel to any of its faces. To make cuts precise, each edge of length $ w $ is cut into the same number of equal parts, each having integer length; similarly for edges of lengths $ h $ and $ d $ . Given the dimensions of the honey cake, determine whether it is possible to cut it into $ n $ equal pieces, and if so, how.

The first line of input contains three integers: $ w $ , $ h $ , and $ d $ , the dimensions of the honey cake in inches ( $ 1 \le w, h, d \le 10^9 $ ). The second line contains a single integer $ n $ ( $ 1 \le n \le 10^9 $ ).

Output three integers $ w_c $ , $ h_c $ , $ d_c $ , the number of cuts to be made along each of the dimensions $ w $ , $ h $ , and $ d $ , respectively, if it is possible to cut the cake, or a single integer $ -1 $ otherwise. Note that making zero cuts along a dimension is allowed, too.

In the first example, the cake will be cut into $ 5 \cdot 4 \cdot 2 = 40 $ pieces of size $ 2 \times 5 \times 3 $ inches.