CF2181I Irrigation Interlock
题目描述
两个灌溉合作社共用一个肥沃的山谷。第一家合作社在田野间维护着若干台泵站;第二家合作社负责监督周围山丘上的水库。每当两个合作社决定分别铺设两根新管道时,这两根管道必须相交——在交点处可以安装一个联合阀门。每根管道总是沿着连接两个不同泵站或两个不同水库的直线段。两根管道若有至少一个公共点,则认为它们相交(无论仅接触还是重合,都算作相交)。
已知每个泵站和每个水库在平面直角坐标系上的精确坐标。对于每个规划方案,判断第一合作社是否能够选出两个不同的泵站、第二合作社是否能够选出两个不同的水库,使得各自连成的两条直线管道相交。如果可能,输出所选泵站和水库的编号;否则,说明该工程无法实现。
输入格式
第一行包含一个整数 $t$($1 \le t \le 10^5$),表示规划方案的数量。
对于每个规划方案:
第一行包含一个整数 $n$($2 \le n \le 10^5$),表示第一合作社管理的泵站数量。
接下来的 $n$ 行,每行包含两个整数 $x_i$ 和 $y_i$($|x_i|, |y_i| \le 10^9$),表示第 $i$ 个泵站的坐标。所有泵站的位置各不相同。
接下来一行包含一个整数 $m$($2 \le m \le 10^5$),表示第二合作社管理的水库数量。
接下来的 $m$ 行,每行包含两个整数 $u_j$ 和 $v_j$($|u_j|, |v_j| \le 10^9$),表示第 $j$ 个水库的坐标。所有水库的位置各不相同。
任意一个泵站的位置都不会与任意一个水库的位置重合。
保证所有规划方案中 $n$ 的总和不超过 $2 \times 10^5$,所有 $m$ 的总和也不超过 $2 \times 10^5$。
输出格式
对于每个规划方案:
如果第一个合作社能选出两个泵站、第二个合作社能选出两个水库,使得各自连线的直线段相交,则输出四个整数 $p_1$、$p_2$、$r_1$、$r_2$——表示所选两个泵站($1 \le p_1, p_2 \le n$,$p_1 \ne p_2$)和所选两个水库($1 \le r_1, r_2 \le m$,$r_1 \ne r_2$)的编号。
如果不存在这样的选择,使得直线相交,则输出 $-1$。
如有多种方案,输出任意一种均可。
说明/提示


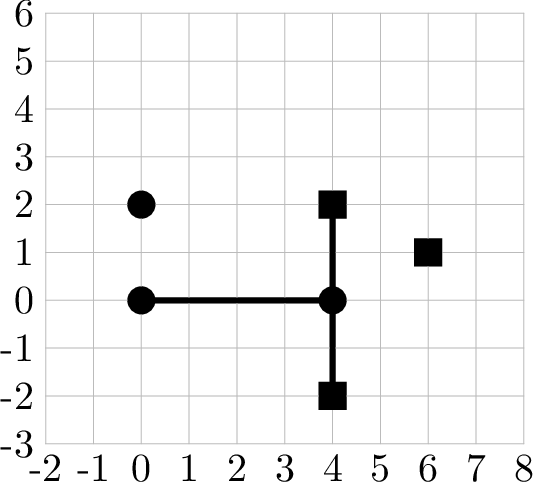
规划方案 1
规划方案 2
规划方案 3
由 ChatGPT 5 翻译