CF2187G Many Cartesian Trees

Consider an array $ a $ consisting of $ n $ distinct integers. The Cartesian Tree of $ a $ is defined as a unique binary tree $ ^{\text{∗}} $ that satisfies the following conditions: - The tree consists of $ n $ vertices labeled from $ 1 $ to $ n $ ; - For all pairs of vertices $ (i,j) $ such that $ i $ is a parent $ ^{\text{†}} $ of $ j $ , $ a_i > a_j $ ; - For any vertex $ i $ , all vertices in the left subtree $ ^{\text{‡}} $ of $ i $ have labels less than $ i $ ; - For any vertex $ i $ , all vertices in the right subtree of $ i $ have labels greater than $ i $ . Denote $ r(a) $ as the root of the Cartesian Tree, and $ f_a(i) $ as the parent of $ i $ in the Cartesian Tree. Define $ E_a=\{(i,f_a(i)) \mid 1 \le i \le n, i \ne r(a)\} $ . 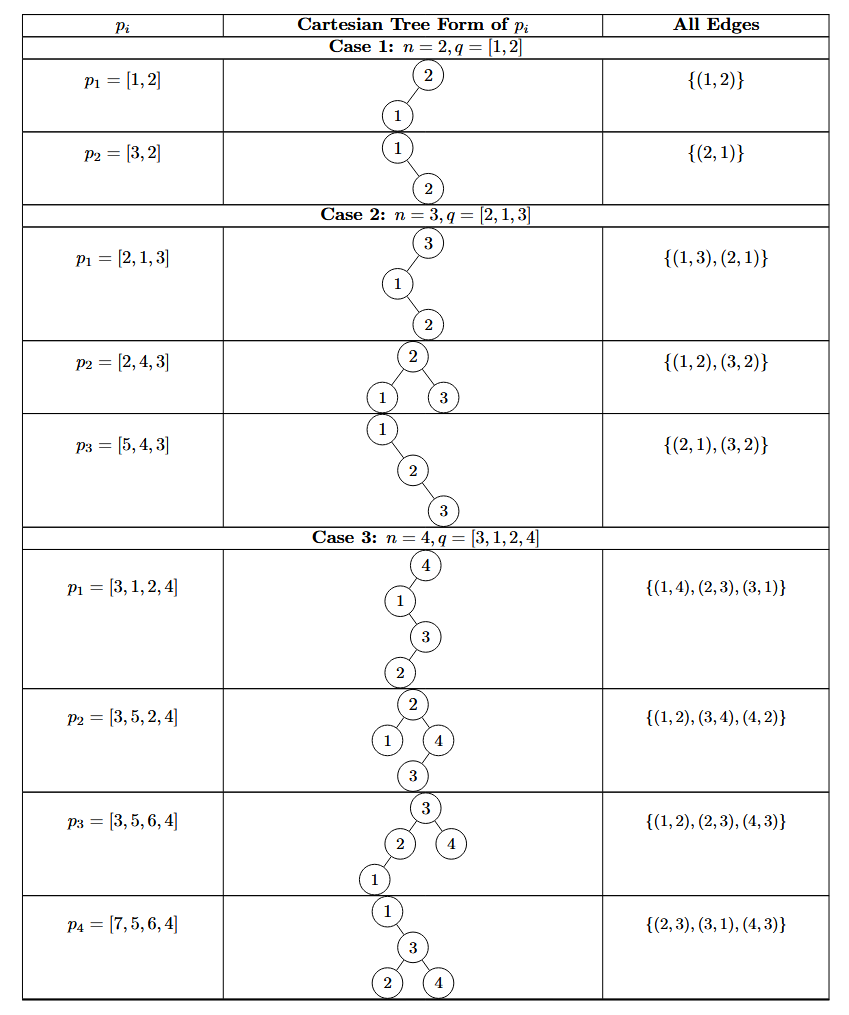Consider a permutation $ ^{\text{§}} $ $ q $ of length $ n $ . We define a series of arrays $ p_1,p_2,\ldots,p_n $ as follows: - $ p_1=q $ ; - For each $ 2 \le i \le n $ , $ p_i $ is obtained by incrementing the minimum element in $ p_{i-1} $ by $ n $ . It can be shown that all elements in $ p_i $ are distinct. You are now given $ n $ and $ S=\bigcup\limits_{i=1}^n E_{p_i} $ . To minimize input, $ S $ will be given in the form of a $ n \times n $ binary matrix $ s $ . Denote $ s_{i,j} $ as the $ j $ -th character of the $ i $ -th row. $ s_{i,j}=1 $ if and only if $ (i,j) \in S $ . Please find any permutation $ q $ such that $ S $ can be obtained by the process above. It is guaranteed that the tests are generated to ensure a valid $ q $ always exists. $ ^{\text{∗}} $ A binary tree is a rooted tree, in which each node has no more than $ 2 $ children, referred to as the left child and the right child. $ ^{\text{†}} $ The parent of vertex $ v $ is the first vertex on the simple path from $ v $ to the root. The root has no parent. $ ^{\text{‡}} $ A subtree of vertex $ v $ is the subgraph of $ v $ , all its descendants, and all the edges between them. $ ^{\text{§}} $ A permutation of length $ n $ is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array), and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array).

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test contains an integer $ n $ ( $ 2 \le n \le 3000 $ ) — the length of $ q $ that you need to find. The $ i $ -th of the next $ n $ lines contains a binary string of length $ n $ , representing the $ i $ -th row of $ s $ . It is guaranteed that $ s_{i,i} = 0 $ for all $ 1 \le i \le n $ . It is guaranteed that the tests are generated to ensure a valid $ q $ always exists. It is guaranteed that the sum of $ n^2 $ over all test cases does not exceed $ 9 \cdot 10^6 $ .

For each test case, output $ n $ integers $ q_1,q_2,\ldots,q_n $ , representing the permutation $ q $ you found.