CF2190D Prufer Vertex

For a tree $ T $ with $ n \ge 2 $ vertices, consider the standard process for generating its [Prufer sequence](https://en.wikipedia.org/wiki/Prufer_sequence). We repeatedly perform the following steps until only two vertices remain: - Select the leaf with the smallest label; - Remove it from the tree. It is known that vertex $ n $ is always one of the two remaining vertices. Let $ v $ be the other remaining vertex. We define the Prufer vertex of $ T $ as $ P(T) = v $ . You are given a forest with $ n $ vertices and $ m $ edges. Let $ k $ be the number of connected components in this forest, and let their sizes be $ s_1, s_2, \ldots, s_k $ . It is known that there are exactly $ n^{k - 2} \prod\limits_{i=1}^k s_i $ ways to add edges to the forest so that it becomes a single tree. For each $ v $ ( $ 1 \le v < n $ ), calculate how many of these ways result in a tree $ T $ satisfying $ P(T) = v $ . Since the answers can be large, print them modulo $ 998\,244\,353 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 0 \le m \le n - 1 $ ) — the number of vertices and edges in the forest, respectively. The next $ m $ lines of each test case contain two integers $ u $ and $ v $ ( $ 1 \le u, v \le n, u \neq v $ ), describing an edge between vertices $ u $ and $ v $ . It is guaranteed that these edges form a forest (that is, the graph is acyclic). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, print $ n - 1 $ integers on a single line. The $ i $ -th integer should be the number of ways to add edges to the forest so that it becomes a tree $ T $ satisfying $ P(T) = i $ , modulo $ 998\,244\,353 $ .

In the first example, there are no edges in the forest, and there are $ 3 $ ways to complete it to a tree. One of them is to add edges $ (1, 2) $ and $ (1, 3) $ . There are $ 2 $ leaves: vertex $ 2 $ and $ 3 $ . Since $ 2 $ has a smaller label, it gets deleted from the tree, and only two vertices remain: $ 1 $ and $ 3 $ . Therefore, the Prufer vertex of this tree is $ 1 $ . 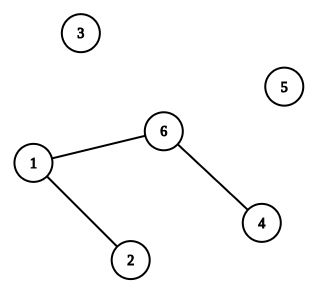In the third example, the forest is shown below:  Suppose we add edges $ (3, 5) $ and $ (3, 1) $ to complete it to a tree $ T $ . 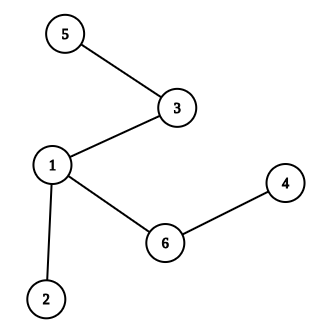It is going to look like this:  It can be shown that $ P(T) = 1 $ .