CF2194F1 Again Trees... (Easy Version)

This is the easy version of the problem. The difference between the versions is that in this version, $ k \leq 4 $ . You can hack only if you solved all versions of this problem. Given a tree consisting of $ n $ vertices. Each vertex has a non-negative integer $ a_v $ written on it. You are also given $ k $ distinct non-negative integers $ b_1, \ldots, b_k $ . We will call a set of edges beautiful if, after removing these edges from the tree, the tree splits into connected components, where in each component the bitwise XOR of all the numbers $ a_v $ in that component belongs to the set $ b $ . You need to count the number of beautiful sets of edges in the tree modulo $ 10^9 + 7 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 500 $ ). The description of the test cases follows. The first line of each dataset contains two integers $ n $ and $ k $ ( $ 2 \leq n \leq 10^5 $ , $ 1 \leq k \leq 4 $ ) — the number of vertices in the tree and the size of the set $ b $ . The next $ n - 1 $ lines describe the edges of the tree. The $ i $ -th line contains two integers $ v_i $ and $ u_i $ ( $ 1 \leq v_i, u_i \leq n $ ) — the numbers of the vertices connected by the $ i $ -th edge. The next line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 0 \leq a_i \lt 2^{30} $ ) — the values written on the vertices. The following line contains $ k $ distinct integers $ b_1, b_2, \ldots, b_k $ ( $ 0 \leq b_i \lt 2^{30} $ ) — the elements of the set $ b $ . It is guaranteed that the sum of $ n $ across all datasets does not exceed $ 10^5 $ .

For each test dataset, output a single integer — the answer to the problem.

Illustration for the first test dataset. In it, you can remove the edge between vertices $ 1 $ and $ 2 $ . Then the bitwise XOR in the component consisting of vertices $ 2 $ and $ 5 $ is $ a_2 \oplus a_5 = 2 \oplus 3 = 1 $ . The bitwise XOR in the component with vertices $ 1 $ , $ 3 $ , and $ 4 $ is $ a_1 \oplus a_3 \oplus a_4 = 0 \oplus 2 \oplus 3 = 1 $ . The second beautiful set is the one consisting of the edge connecting vertices $ 1 $ and $ 3 $ . 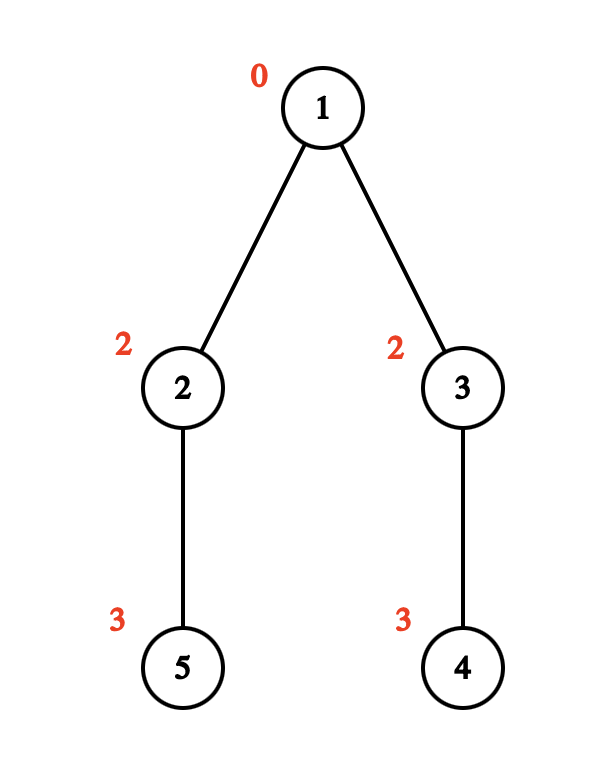In the third test dataset, the beautiful sets will be (an edge is denoted by the pair of vertices it connects) $ [(1, 2)], [(1, 3)], [(2, 5)], [(3, 4)] $ . Note that the first and third samples differ only in the set $ b $ . In the fourth test dataset, the beautiful sets will be $ [(1, 2)], [(3, 4)], [(1, 2), (2, 3), (3, 4)] $ .