CF225E Unsolvable

Consider the following equation: 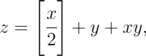 where sign $ [a] $ represents the integer part of number $ a $ .Let's find all integer $ z $ $ (z>0) $ , for which this equation is unsolvable in positive integers. The phrase "unsolvable in positive integers" means that there are no such positive integers $ x $ and $ y $ $ (x,y>0) $ , for which the given above equation holds. Let's write out all such $ z $ in the increasing order: $ z_{1},z_{2},z_{3} $ , and so on $ (z_{i}<z_{i+1}) $ . Your task is: given the number $ n $ , find the number $ z_{n} $ .

The first line contains a single integer $ n $ ( $ 1

Print a single integer — the number $ z_{n} $ modulo $ 1000000007 $ $ (10^{9}+7) $ . It is guaranteed that the answer exists.