CF225E Unsolvable
题目描述
考虑如下方程:
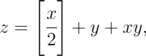
其中 $\operatorname{sign}[a]$ 表示 $a$ 的整数部分。我们要求所有正整数 $z$(即 $z>0$),使得该方程在正整数中无解。这里“在正整数中无解”是指不存在正整数 $x$ 和 $y$(即 $x,y>0$),使上述方程成立。
请将所有满足条件的 $z$ 按递增顺序排列为 $z_1, z_2, z_3, \ldots$(满足 $z_i < z_{i+1}$)。你的任务是:给定一个数 $n$,求出第 $n$ 小的这样的 $z$,即 $z_n$。
输入格式
第一行为一个整数 $n$($1 \leq n \leq 40$)。
输出格式
输出一个整数,表示 $z_n \bmod 1000000007$($10^9+7$)。保证答案一定存在。
说明/提示
由 ChatGPT 5 翻译