CF231D Magic Box

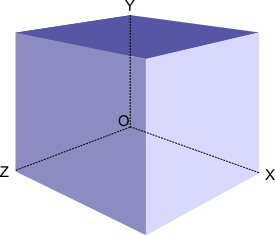
有一天，Vasya 回家时在路上看见了一个盒子。这个盒子可以表示为一个长方体。Vasya 很快意识到，这个盒子很特别，因为它的所有边都平行于坐标轴，其中一个顶点在点 $(0,0,0)$，另一个对角顶点在点 $(x_{1},y_{1},z_{1})$。盒子的六个面上各写有一个数字 $a_{1},a_{2},...,a_{6}$，每个数字位于每个面的正中心。   这些数字在盒子上的分布如下： - 数字 $a_{1}$ 写在位于 $ZOX$ 平面上的面上； - $a_{2}$ 写在与上述平面平行的另一个面上； - $a_{3}$ 写在位于 $XOY$ 平面上的面上； - $a_{4}$ 写在与上述平面平行的另一个面上； - $a_{5}$ 写在位于 $YOZ$ 平面上的面上； - $a_{6}$ 写在与上述平面平行的另一个面上。 此刻 Vasya 从点 $(x, y, z)$ 观察这个盒子。请你计算 Vasya 能看到的数字的和。注意，盒子的所有面都是不透明的，Vasya 不能透过盒子看到数字。图中将部分面画成透明，仅为方便理解。你可以认为，如果 Vasya 观察的位置正好在某个面的平面上，他是无法看到该面中心的数字的。对于 Vasya 来说，只要能看到某一面的中心，就能看到该面上的数字。此外，Vasya 总是能正确读出他所看的 $a_{i}$ 数字，不会因旋转、视角等产生混淆（例如，看到 $a_{i}=6$ 时，不会误认为是 $9$ 等）。

第一行包含三个用空格分隔的整数 $x, y, z$（$|x|,|y|,|z| \le 10^{6}$），表示 Vasya 在空间中的坐标。 第二行包含三个用空格分隔的整数 $x_{1}, y_{1}, z_{1}$（$1 \le x_{1}, y_{1}, z_{1} \le 10^{6}$），表示盒子在 $(0,0,0)$ 的对角顶点的坐标。 第三行包含六个用空格分隔的整数 $a_{1},a_{2},...,a_{6}$（$1 \le a_{i} \le 10^{6}$），表示盒子六个面上的数字。 保证点 $(x,y,z)$ 严格在盒子外部。

输出一个整数，表示 Vasya 能看到的所有盒子面上的数字之和。

第一个样例对应图片所展示的视角。Vasya 能看到 $a_{2}$（最暗的顶面），$a_{6}$（最亮的右面）和 $a_{4}$（左侧可见的面）。 在第二个样例中，Vasya 只能看到 $a_{4}$。 由 ChatGPT 5 翻译