CF232B Table

John Doe 有一个 $n \times m$ 的表格。John Doe 可以在表格的某些单元格内画点，每个单元格最多只能画一个点。 John Doe 想用这样的操作，使得每一个大小为 $n \times n$ 的正方形子表格中恰好有 $k$ 个点。 John Doe 想知道，有多少种不同的方式可以在表格中放置点，使上述条件成立。由于这个数可能非常大，John Doe 要求你输出这个数对 $1000000007$ $(10^9+7)$ 取模后的结果。 你可以认为 John 总是将点画在某个单元格的正中央。如果有一个单元格在一种方式下有点，而在另一种方式下没有点，那么这两种填法被认为是不同的。

一行包含用空格分隔的三个整数 $n$、$m$、$k$（$1 \le n \le 100;\ n \le m \le 10^{18};\ 0 \le k \le n^2$）——表格的行数、列数以及每个正方形中需要的点数。 请不要在 C++ 中用 %lld 读写 64 位整数。推荐使用 cin、cout 流或 %I64d。

输出一个整数，表示满足条件的方案数对 $1000000007$ $(10^9+7)$ 取模后的结果。

以第一个测试样例为例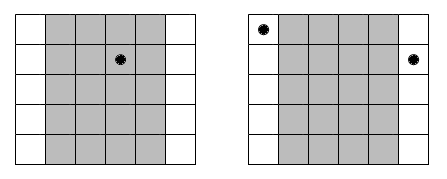：  灰色区域属于两个 $5\times5$ 的正方形。如果灰色区域有一个点，那么其它位置不应再有点。如果其中一个白色区域有一个点，另一个也必须有一个点。因此，大约有 $20$ 种点在灰色区域的方案，还有 $25$ 种每个白色区域有一个点的方案。总共有 $45$ 种方案。 由 ChatGPT 5 翻译